Lesson 25: Solving Problems in Two Ways Rates and Algebra
|
|
|
- Leo Sullivan
- 5 years ago
- Views:
Transcription
1 : Solving Problems in Two Ways Rates and Algebra Student Outcomes Students investigate a problem that can be solved by reasoning quantitatively and by creating equations in one variable. They compare the numerical approach to the algebraic approach. Classwork Opening (10 minutes) Exercise 1 MP.2 1. Solve the following problem first using a tape diagram and then using an equation: In a school choir, ½ of the members were girls. At the end of the year, 3 boys left the choir and the ratio of the number of boys to the number of girls became 3:4. How many boys remained in the choir? Date: 7/10/13 265
2 2. Which problem solution, the one using a tape diagram or the one using an equation, was easier to set up and solve? Why? Answers will vary. Most will say the tape diagram. It required significantly less work than solving the problem algebraically. Point out that this may not always be the case. Ask students how to modify the question in such a way that the tape diagram solution would definitely not be the easier way to solve the problem. Sample answer: In a school choir, 6/11 of the members were girls. At the end of the year, 3 boys had left the choir and the ratio of the number of boys to the number of girls was 3:4. How many boys remained in the choir? Discussion (30 minutes) MP.1 The following problem is nontrivial for students. Please study the different solution types carefully before working the problem with your students. Always let students work (individually or in groups of 2) on each solution type for 5-10 minutes before summarizing with the entire class. While they are working, walk around and help, looking for students or groups who could present a correct solution (or could present a solution with your guidance). If no one gets the problem, that s okay. Their struggle has prepared them to understand the issues involved in the problem as they work through it with you. Exercise 2 a. Read the following problem: All the printing presses at a print shop were scheduled to make copies of a novel and a cookbook. They were to print the same number of copies of each book, but the novel had twice as many pages as the cookbook. All of the printing presses worked for the first day on the larger book, turning out novels. Then, on day 2, the presses were split into two equally sized groups. The first group continued printing copies of the novel and finished printing all the copies by the evening of the second day. The second group worked on the cookbook, but did not finish by evening. One printing press, working for two additional full days, finished printing the remaining copies of the cookbooks. If all printing presses printed pages (for both the novel and cookbook) at the same constant rate, how many printing presses are there at the print shop? Analyze the problem with your students, rereading the problem together as you answer questions like: What is this story about? [Printing novels and cookbooks.] Will more novels be printed than cookbooks, or less? [Neither. The same number of each.] How many pages does the novel have compared to the cookbook? [Twice as many as the cookbook] How much longer would one printing press take to print a novel versus a cookbook? [Twice as long] Do you think it is important to know how many pages each book has, or how many of each book will need to be printed? Why? [No. Answers will vary.] How many of the printing presses are used to print the novel on the first day? [All of them] How many of the printing presses are used to print the novel on the second day? [1/2 of them] How many of the printing presses are used to print the cookbook on the second day? [1/2 of them] Date: 7/10/13 266
3 How many printing presses are used to print the remainder of the cookbooks on the third and fourth day? [1] How many printing presses could be used to print the remainder of the cookbooks in one day instead of two? [2 printing presses could have finished the cookbooks on the third day.] What are we trying to find in this problem? [The number of printing presses at the print shop.] b. Solve the problem in Exercise 2a working with rates to setup a tape diagram or an area model. One of the keys to a (somewhat) simple solution using an area model is recognizing that the novel has twice as many pages as the cookbook, so the area that represents the novel job should be twice the size as the area used to represent the cookbook job. Draw a rectangular region to represent the work needed to complete the novel job and another rectangular region, half the size, to represent the work needed to complete the cookbook job. On the first day, all the printers were used on printing copies of the novel, and on the second day, half completed the novel and half worked on the cookbook. Students can test conjectures on why the novel job is split into thirds. For example, if all printers completed of the novel job on day 1, then of the printers would only complete of the job on day 2. So only of the novel job would be complete by the end of day 2. But the story says the whole novel job is complete by the end of day 2, i.e., something is wrong with that conjecture. Date: 7/10/13 267
4 Once students understand that the novel job must be split into thirds, label the novel job, the whole unit, and each third unit as the fractional unit, of the whole. The cookbook job is then of the whole. The same unit must have also been completed on the cookbook job on day 2, leaving = of the whole unit left for days 3 and 4. Each of the small rectangles in the picture above represents how much of the whole job (i.e., novel job) 1 printer can do in 1 day. Drawing in the small rectangle units into the rest of the diagram, one sees that 8 printers worked on the novel job on day 1, which was all of the printers. Hence, there are 8 printers at the print shop! Students now know there are 8 printers at the workshop. This should help them confirm their solution paths in Exercise 2c! 3. Solve the problem in Exercise 2a by setting up an equation. MP.2 Start by asking students to write down all variables for the quantities they see in the problem, giving an appropriate letter for each. While it doesn t matter if they work with the number of copies of cookbooks, or the number of pages per cookbook, guide them to use the number of copies of cookbooks as you walk around your class. (Tell students not to worry about writing down too many letters there is no need to write all of them.) Be careful not to write on the board, printers =. Such a statement abuses how the = symbol should be used. Such statements do not make sense printers aren t numbers! It is a good idea to require students to develop the habit of always properly labeling their variables using short descriptions like, # of printers:. This habit can significantly help them in setting up equations and solving algebra problems. # of printers:. This is what we wish to find! # of copies of cookbooks printed by 1 printer in 1 day:. # of copies of novels printed by 1 printer in 1 day:. Only half the number of novels can be produced each day. # of copies in the cookbook job:. # of copies in the novel job:. Date: 7/10/13 268
5 Next, ask students to write down important expressions using the variables above. There are many valid possible expressions they can write down that can be used to solve the problem. Here is one possible list: Novels: # of copies of novels printed in 1 day by the entire print shop:. # of copies of novels printed in 1 day by half of the entire print shop:. Total number of copies of novels printed:, or. Cookbooks: # of copies of cookbooks printed in 1 day by half of the entire print shop:. # of copies of cookbooks printed in 2 days by 1 printer:. Total number of copies of cookbooks printed:. Since the number of cookbooks and novels is the same, we can equate the expressions of the totals above to get: Since is known not to be zero, we can divide both sides of the equation by, and solve the resulting equation for : Check by substituting 8 back into the original equation: The left hand side is which is equal to the right hand side, Date: 7/10/13 269
6 There are 8 printers in the print shop! MP.1 Students will inevitably create several solution paths. That is because there are a number of ways to setup a correct equation. If time permits, explore the different solution paths with students. Help them see that their solution is just as valid as the teacher s. Closing (5 minutes) Discuss the following questions with your students: Why is this problem not about a real situation? That is, how can you tell it was completely made up? The clue it is a made up problem is the question: why would the number of printers not be known in this situation? In a real life situation, not only would the number of printing presses be known, but the constant speed in which they print pages would be known too. Plus, the number of pages in each book would certainly be a big part of figuring out how to schedule the job, as well as knowing exactly how many copies each client wanted. Tell students that the problem was purposely made up in order to ask the following exit ticket question. Exit Ticket (5 minutes) Date: 7/10/13 270
7 Name Date Exit Ticket Suppose we know that the print shop had 8 printing presses and each printing press runs at a constant speed of 5000 pages per hour for 6 hours a day. 1. Compute the total number of pages printed for the cookbook job and the total number of pages printed for the novel job following the schedule and situation described in Exercise 2a. 2. Describe a scenario where it would make sense for the job scheduler to schedule both jobs as described in Exercise 2a. 3. BONUS: If the novel was 500 pages and the cookbook 250 pages, how many copies of each were printed? Date: 7/10/13 266
8 Exit Ticket Sample Solutions Suppose we know that the print shop had 8 printing presses and each printing press runs at a constant speed of 5000 pages per hour for 6 hours a day. 1. Compute the total number of pages printed for the cookbook job and the total number of pages printed for the novel job following the schedule and situation described in Exercise 2a. # of pages printed by a printer in 1 day: 30,000 # of pages printed by 8 printers in 1 day: 240,000 # of pages printed by 8 printers in 2 days: 480,000 # of pages 1 printer prints in 2 days: 60,000 # of pages printed for both jobs: 60, ,000 = 540,000. Ratio of number of pages of the novel to the number of pages of the cookbook: 2:1. Hence, 360,000 pages for the novel, 180,000 for the cookbook. 2. Describe a scenario where it would make sense for the job scheduler to schedule both jobs as describe in Exercise 2a. The client for the novel job wants the print job completed by midweek, whereas the cookbook doesn t need to be completed until the end of the week. 3. BONUS: if the novel was 250 pages and the cookbook 125 pages, how many copies of each were printed? 1440 copies of each were printed. Problem Set Sample Solutions 1. Solve the following problems first using a tape diagram, then by setting up an equation. For each, give your opinion on which solution method was easier. Can you see the connection(s) between the two methods? What does each unit in the tape diagram stand for? a. 16 years from now, Pia s age will be twice her age 12 years ago. Find her present age. Tape: Date: 7/10/13 267
9 Equation: b. The total age of a woman and her son is 51 years. Three years ago, the woman was 8 times as old as her son. How old is her son now? Tape: Equation: Date: 7/10/13 268
10 c. Five years from now, the sum of the ages of a woman and her daughter will be 40 years. The difference in their present age is 24 years. How old is her daughter now? Tape: Equation: d. Find three consecutive integers such that their sum is 51. Tape: Date: 7/10/13 269
11 Equation: 4. Solve the following problems by setting up an equation or inequality. a. If two numbers represented by and have a sum of, find. Date: 7/10/13 270
12 b. Find two consecutive even numbers such that the sum of the smaller number and twice the greater number is 100. c. If 9 is subtracted from a number, and the result is multiplied by 19, the product is 171. Find the number. Date: 7/10/13 271
13 d. The product of two consecutive whole numbers is less than the sum of the square of the smaller number and The length, 18 meters, is the answer to the following question. The length of a rectangle is 3 meters longer than its width. The area of the rectangle is 270 square meters. What is the length of the rectangle? Rework this problem: Write an equation using be the length (in meters) of the rectangle that would lead to the solution of the problem. Check that the answer above is correct by substituting 18 for in your equation. Length (in meters): Width (in meters): Equation: Check: 6. Jim tells you he paid a total of $23, for a car, and you would like to know the price of the car before sales tax so that you can compare the price of that model of car at various dealers. Find price of the car before sales tax if Jim bought the car in: a. Arizona, where the sales tax is 6.6%. Solving results in. The car costs $21,650. b. New York, where the sales tax is 8.25%. Solving results in. The car costs $21,320. c. A state where the sales tax is %. Solving results in. For a sales tax of s%, the car costs dollars. Date: 7/10/13 272
14 7. A checking account is set up with an initial balance of $9400, and $800 is removed from the account at the end of each month for rent (no other user transactions occur on the account). a. Write an inequality whose solutions are the months,, in which the account balance is greater than $3000. Write the solution set to your equation by identifying all of the solutions. For a non-negative real number, satisfies the inequality,. For real numbers, the solution set is. b. Make a graph of the balance in the account after months and indicate on the plot the solutions to your inequality in part (a). Students can create a step-function (like below), or simply plot the points (with no lines drawn). Drawing a straight line through the points, however, does not accurately reflect the information in the problem. 8. Axel and his brother like to play tennis. About three months ago they decided to keep track of how many games they have each won. As of today, Axel has won 18 out of the 30 games against his brother. a. How many games would Axel have to win in a row in order to have a 75% winning record? Solving,, results in. He would have to win 18 games. b. How many games would Axel have to win in a row in order to have a 90% winning record? Solving,, results in. He would have to win 90 games. c. Is Axel ever able to reach a 100% winning record? Explain why or why not. No. A 100% winning record would mean solving the equation,, which has no solutions. Date: 7/10/13 273
15 d. Suppose that after reaching a winning record of 90% in part (b), Axel had a losing streak. How many games in a row would Axel have to lose in order to drop down to a winning record of 60% again? Solving,, results in. He would have to lose 60 games. 9. Omar has $84 and Calina has $12. How much money must Omar give to Calina so that Calina will have 3 times as much as Omar? a. Solve the problem above by setting up an equation. Solution 1: Amount Omar gives: dollars. Amount Omar has after giving:. Amount Calina has after:. Equation: Solve: Check: Omar now has $24 and Calina has $72, which is 3 times as much as Omar. Solution 2: A few students might notice that if Calina has 3 times as much as Omar afterwards, and if we let be the amount that Omar has after, then, or. Now it is easy to find out how much Omar gave. b. In your opinion, is this problem easier to solve using an equation, or using a tape diagram? Why? Most likely, students will say it is easier to solve with an equation because it is easier to setup and solve. (They may show an attempt at drawing a tape diagram, for example.) However, students who used the second solution may respond that the tape diagram is easier. Date: 7/10/13 274
AskDrCallahan Calculus 1 Teacher s Guide
 AskDrCallahan Calculus 1 Teacher s Guide 3rd Edition rev 080108 Dale Callahan, Ph.D., P.E. Lea Callahan, MSEE, P.E. Copyright 2008, AskDrCallahan, LLC v3-r080108 www.askdrcallahan.com 2 Welcome to AskDrCallahan
AskDrCallahan Calculus 1 Teacher s Guide 3rd Edition rev 080108 Dale Callahan, Ph.D., P.E. Lea Callahan, MSEE, P.E. Copyright 2008, AskDrCallahan, LLC v3-r080108 www.askdrcallahan.com 2 Welcome to AskDrCallahan
Bite Size Brownies. Designed by: Jonathan Thompson George Mason University, COMPLETE Math
 Bite Size Brownies Designed by: Jonathan Thompson George Mason University, COMPLETE Math The Task Mr. Brown E. Pan recently opened a new business making brownies called The Brown E. Pan. On his first day
Bite Size Brownies Designed by: Jonathan Thompson George Mason University, COMPLETE Math The Task Mr. Brown E. Pan recently opened a new business making brownies called The Brown E. Pan. On his first day
North Carolina Standard Course of Study - Mathematics
 A Correlation of To the North Carolina Standard Course of Study - Mathematics Grade 4 A Correlation of, Grade 4 Units Unit 1 - Arrays, Factors, and Multiplicative Comparison Unit 2 - Generating and Representing
A Correlation of To the North Carolina Standard Course of Study - Mathematics Grade 4 A Correlation of, Grade 4 Units Unit 1 - Arrays, Factors, and Multiplicative Comparison Unit 2 - Generating and Representing
Mobile Math Teachers Circle The Return of the iclicker
 Mobile Math Teachers Circle The Return of the iclicker June 20, 2016 1. Dr. Spock asked his class to solve a percent problem, Julia set up the proportion: 4/5 = x/100. She then cross-multiplied to solve
Mobile Math Teachers Circle The Return of the iclicker June 20, 2016 1. Dr. Spock asked his class to solve a percent problem, Julia set up the proportion: 4/5 = x/100. She then cross-multiplied to solve
Proofs That Are Not Valid. Identify errors in proofs. Area = 65. Area = 64. Since I used the same tiles: 64 = 65
 1.5 Proofs That Are Not Valid YOU WILL NEED grid paper ruler scissors EXPLORE Consider the following statement: There are tthree errorss in this sentence. Is the statement valid? GOAL Identify errors in
1.5 Proofs That Are Not Valid YOU WILL NEED grid paper ruler scissors EXPLORE Consider the following statement: There are tthree errorss in this sentence. Is the statement valid? GOAL Identify errors in
d. Could you represent the profit for n copies in other different ways?
 Special Topics: U3. L3. Inv 1 Name: Homework: Math XL Unit 3 HW 9/28-10/2 (Due Friday, 10/2, by 11:59 pm) Lesson Target: Write multiple expressions to represent a variable quantity from a real world situation.
Special Topics: U3. L3. Inv 1 Name: Homework: Math XL Unit 3 HW 9/28-10/2 (Due Friday, 10/2, by 11:59 pm) Lesson Target: Write multiple expressions to represent a variable quantity from a real world situation.
DIFFERENTIATE SOMETHING AT THE VERY BEGINNING THE COURSE I'LL ADD YOU QUESTIONS USING THEM. BUT PARTICULAR QUESTIONS AS YOU'LL SEE
 1 MATH 16A LECTURE. OCTOBER 28, 2008. PROFESSOR: SO LET ME START WITH SOMETHING I'M SURE YOU ALL WANT TO HEAR ABOUT WHICH IS THE MIDTERM. THE NEXT MIDTERM. IT'S COMING UP, NOT THIS WEEK BUT THE NEXT WEEK.
1 MATH 16A LECTURE. OCTOBER 28, 2008. PROFESSOR: SO LET ME START WITH SOMETHING I'M SURE YOU ALL WANT TO HEAR ABOUT WHICH IS THE MIDTERM. THE NEXT MIDTERM. IT'S COMING UP, NOT THIS WEEK BUT THE NEXT WEEK.
Student Outcomes. Classwork. Fluency Exercise (5 minutes) Mathematical Modeling Exercise (6 minutes)
 Lesson 28: Two Step Problems All Operations Student Outcomes Students calculate the solution of one step equations by using their knowledge of order of operations and the properties of equality for addition,
Lesson 28: Two Step Problems All Operations Student Outcomes Students calculate the solution of one step equations by using their knowledge of order of operations and the properties of equality for addition,
GCSE Mathematics Practice Tests: Set 1
 GCSE Mathematics Practice Tests: Set 1 Paper 2F (Calculator) Time: 1 hour 30 minutes You should have: Ruler graduated in centimetres and millimetres, protractor, pair of compasses, pen, HB pencil, eraser,
GCSE Mathematics Practice Tests: Set 1 Paper 2F (Calculator) Time: 1 hour 30 minutes You should have: Ruler graduated in centimetres and millimetres, protractor, pair of compasses, pen, HB pencil, eraser,
MA 15910, Lesson 5, Algebra part of text, Sections 2.3, 2.4, and 7.5 Solving Applied Problems
 MA 15910, Lesson 5, Algebra part of text, Sections 2.3, 2.4, and 7.5 Solving Applied Problems Steps for solving an applied problem 1. Read the problem; carefully noting the information given and the questions
MA 15910, Lesson 5, Algebra part of text, Sections 2.3, 2.4, and 7.5 Solving Applied Problems Steps for solving an applied problem 1. Read the problem; carefully noting the information given and the questions
Overview. Teacher s Manual and reproductions of student worksheets to support the following lesson objective:
 Overview Lesson Plan #1 Title: Ace it! Lesson Nine Attached Supporting Documents for Plan #1: Teacher s Manual and reproductions of student worksheets to support the following lesson objective: Find products
Overview Lesson Plan #1 Title: Ace it! Lesson Nine Attached Supporting Documents for Plan #1: Teacher s Manual and reproductions of student worksheets to support the following lesson objective: Find products
Table of Contents. Introduction...v. About the CD-ROM...vi. Standards Correlations... vii. Ratios and Proportional Relationships...
 Table of Contents Introduction...v About the CD-ROM...vi Standards Correlations... vii Ratios and Proportional Relationships... 1 The Number System... 10 Expressions and Equations... 23 Geometry... 27
Table of Contents Introduction...v About the CD-ROM...vi Standards Correlations... vii Ratios and Proportional Relationships... 1 The Number System... 10 Expressions and Equations... 23 Geometry... 27
Kaytee s Contest Problem https://www.nctm.org/pows/
 Pre-Algebra PoW Packet Kaytee s Contest Problem 16004 https://www.nctm.org/pows/ Welcome! This packet contains a copy of the problem, the answer check, our solutions, some teaching suggestions, and samples
Pre-Algebra PoW Packet Kaytee s Contest Problem 16004 https://www.nctm.org/pows/ Welcome! This packet contains a copy of the problem, the answer check, our solutions, some teaching suggestions, and samples
Sandwich. Reuben BLT. Egg salad. Roast beef
 3.2 Writing Expressions represents an unknown quantity? How can you write an expression that 1 ACTIVITY: Ordering Lunch Work with a partner. You use a $20 bill to buy lunch at a café. You order a sandwich
3.2 Writing Expressions represents an unknown quantity? How can you write an expression that 1 ACTIVITY: Ordering Lunch Work with a partner. You use a $20 bill to buy lunch at a café. You order a sandwich
Lesson 7: Measuring Variability for Skewed Distributions (Interquartile Range)
 : Measuring Variability for Skewed Distributions (Interquartile Range) Student Outcomes Students explain why a median is a better description of a typical value for a skewed distribution. Students calculate
: Measuring Variability for Skewed Distributions (Interquartile Range) Student Outcomes Students explain why a median is a better description of a typical value for a skewed distribution. Students calculate
The Product of Two Negative Numbers 1
 1. The Story 1.1 Plus and minus as locations The Product of Two Negative Numbers 1 K. P. Mohanan 2 nd March 2009 When my daughter Ammu was seven years old, I introduced her to the concept of negative numbers
1. The Story 1.1 Plus and minus as locations The Product of Two Negative Numbers 1 K. P. Mohanan 2 nd March 2009 When my daughter Ammu was seven years old, I introduced her to the concept of negative numbers
Module 1. Ratios and Proportional Relationships Lessons 11 14
 Math 7 Module Lessons.notebook September, 05 Module Ratios and Proportional Relationships Lessons Lesson # September, 05 You need: pencil, calculator and binder. Do Now: Find your group and complete do
Math 7 Module Lessons.notebook September, 05 Module Ratios and Proportional Relationships Lessons Lesson # September, 05 You need: pencil, calculator and binder. Do Now: Find your group and complete do
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWare http://ocw.mit.edu 18.06 Linear Algebra, Spring 2005 Please use the following citation format: Gilbert Strang, 18.06 Linear Algebra, Spring 2005. (Massachusetts Institute of Technology:
MIT OpenCourseWare http://ocw.mit.edu 18.06 Linear Algebra, Spring 2005 Please use the following citation format: Gilbert Strang, 18.06 Linear Algebra, Spring 2005. (Massachusetts Institute of Technology:
EOC FINAL REVIEW Name Due Date
 1. The line has endpoints L(-8, -2) and N(4, 2) and midpoint M. What is the equation of the line perpendicular to and passing through M? A. B. Y= C. Y= D. Y= 3x + 6 2. A rectangle has vertices at (-5,3),
1. The line has endpoints L(-8, -2) and N(4, 2) and midpoint M. What is the equation of the line perpendicular to and passing through M? A. B. Y= C. Y= D. Y= 3x + 6 2. A rectangle has vertices at (-5,3),
MITOCW big_picture_integrals_512kb-mp4
 MITOCW big_picture_integrals_512kb-mp4 PROFESSOR: Hi. Well, if you're ready, this will be the other big side of calculus. We still have two functions, as before. Let me call them the height and the slope:
MITOCW big_picture_integrals_512kb-mp4 PROFESSOR: Hi. Well, if you're ready, this will be the other big side of calculus. We still have two functions, as before. Let me call them the height and the slope:
Correlation to the Common Core State Standards
 Correlation to the Common Core State Standards Go Math! 2011 Grade 4 Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Correlation to the Common Core State Standards Go Math! 2011 Grade 4 Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Lesson 10. Here are the first two worked out.
 Lesson 10 This page is on word problems. They will be using multiplication, division, addition, and subtraction. They will need to take multiple steps to find the answer to the question. They could use
Lesson 10 This page is on word problems. They will be using multiplication, division, addition, and subtraction. They will need to take multiple steps to find the answer to the question. They could use
EIGHTH GRADE RELIGION
 EIGHTH GRADE RELIGION MORALITY ~ Your child knows that to be human we must be moral. knows there is a power of goodness in each of us. knows the purpose of moral life is happiness. knows a moral person
EIGHTH GRADE RELIGION MORALITY ~ Your child knows that to be human we must be moral. knows there is a power of goodness in each of us. knows the purpose of moral life is happiness. knows a moral person
(1) + 1(0.1) + 7(0.001)
 Name: Quarterly 1 Study Guide The first quarterly test covers information from Modules 1, 2, and 3. If you complete this study guide and turn it in on Tuesday, you will receive 5 bonus points on your Quarterly
Name: Quarterly 1 Study Guide The first quarterly test covers information from Modules 1, 2, and 3. If you complete this study guide and turn it in on Tuesday, you will receive 5 bonus points on your Quarterly
1.1 The Language of Mathematics Expressions versus Sentences
 . The Language of Mathematics Expressions versus Sentences a hypothetical situation the importance of language Study Strategies for Students of Mathematics characteristics of the language of mathematics
. The Language of Mathematics Expressions versus Sentences a hypothetical situation the importance of language Study Strategies for Students of Mathematics characteristics of the language of mathematics
Ratios. How are the numbers in each ad compared? Which ads are most effective?
 5 and part to part, part to whole versions of ratios There are different ways to compare numbers. Look @ these advertisments. How are the numbers in each ad compared? Which ads are most effective? 1 5
5 and part to part, part to whole versions of ratios There are different ways to compare numbers. Look @ these advertisments. How are the numbers in each ad compared? Which ads are most effective? 1 5
The Definition of 'db' and 'dbm'
 P a g e 1 Handout 1 EE442 Spring Semester The Definition of 'db' and 'dbm' A decibel (db) in electrical engineering is defined as 10 times the base-10 logarithm of a ratio between two power levels; e.g.,
P a g e 1 Handout 1 EE442 Spring Semester The Definition of 'db' and 'dbm' A decibel (db) in electrical engineering is defined as 10 times the base-10 logarithm of a ratio between two power levels; e.g.,
Unit 7, Lesson 1: Exponent Review
 Unit 7, Lesson 1: Exponent Review 1. Write each expression using an exponent: a. b. c. d. The number of coins Jada will have on the eighth day, if Jada starts with one coin and the number of coins doubles
Unit 7, Lesson 1: Exponent Review 1. Write each expression using an exponent: a. b. c. d. The number of coins Jada will have on the eighth day, if Jada starts with one coin and the number of coins doubles
6-5 Solving Proportions
 Solve each proportion. 24 12.6 34 esolutions Manual - Powered by Cognero Page 1 2.4 29 55 esolutions Manual - Powered by Cognero Page 2 TELEVISION Aspect ratio is the ratio of width to height of a television
Solve each proportion. 24 12.6 34 esolutions Manual - Powered by Cognero Page 1 2.4 29 55 esolutions Manual - Powered by Cognero Page 2 TELEVISION Aspect ratio is the ratio of width to height of a television
TeeJay Publishers. Curriculum for Excellence. Course Planner - Level 1
 TeeJay Publishers Curriculum for Excellence Course Planner Level 1 To help schools develop their courses, TeeJay Publishers has produced a Course Planner for CfE Level 1. This Planner from TeeJay provides
TeeJay Publishers Curriculum for Excellence Course Planner Level 1 To help schools develop their courses, TeeJay Publishers has produced a Course Planner for CfE Level 1. This Planner from TeeJay provides
Example the number 21 has the following pairs of squares and numbers that produce this sum.
 by Philip G Jackson info@simplicityinstinct.com P O Box 10240, Dominion Road, Mt Eden 1446, Auckland, New Zealand Abstract Four simple attributes of Prime Numbers are shown, including one that although
by Philip G Jackson info@simplicityinstinct.com P O Box 10240, Dominion Road, Mt Eden 1446, Auckland, New Zealand Abstract Four simple attributes of Prime Numbers are shown, including one that although
Algebra I Module 2 Lessons 1 19
 Eureka Math 2015 2016 Algebra I Module 2 Lessons 1 19 Eureka Math, Published by the non-profit Great Minds. Copyright 2015 Great Minds. No part of this work may be reproduced, distributed, modified, sold,
Eureka Math 2015 2016 Algebra I Module 2 Lessons 1 19 Eureka Math, Published by the non-profit Great Minds. Copyright 2015 Great Minds. No part of this work may be reproduced, distributed, modified, sold,
Kaytee s Contest. Problem of the Week Teacher Packet. Answer Check
 Problem of the Week Teacher Packet Kaytee s Contest Farmer Kaytee brought one of her prize-winning cows to the state fair, along with its calf. In order to get people to stop and admire her cow, she thought
Problem of the Week Teacher Packet Kaytee s Contest Farmer Kaytee brought one of her prize-winning cows to the state fair, along with its calf. In order to get people to stop and admire her cow, she thought
Warm-up: Thinking back to the chart from Friday, explain how you changed a number in scientific notation to standard form.
 November 4, 2013 LEQ: How can you represent very large and very small numbers in an easier way? Warm-up: Thinking back to the chart from Friday, explain how you changed a number in scientific notation
November 4, 2013 LEQ: How can you represent very large and very small numbers in an easier way? Warm-up: Thinking back to the chart from Friday, explain how you changed a number in scientific notation
SPIRE MATHS Stimulating, Practical, Interesting, Relevant, Enjoyable Maths For All
 Ratio and proportion TYPE: Main OBJECTIVE(S): Understand the relationship between ratio and proportion; use ratio notation, reduce a ratio to its simplest form and divide a quantity into two parts in a
Ratio and proportion TYPE: Main OBJECTIVE(S): Understand the relationship between ratio and proportion; use ratio notation, reduce a ratio to its simplest form and divide a quantity into two parts in a
SEVENTH GRADE. Revised June Billings Public Schools Correlation and Pacing Guide Math - McDougal Littell Middle School Math 2004
 SEVENTH GRADE June 2010 Billings Public Schools Correlation and Guide Math - McDougal Littell Middle School Math 2004 (Chapter Order: 1, 6, 2, 4, 5, 13, 3, 7, 8, 9, 10, 11, 12 Chapter 1 Number Sense, Patterns,
SEVENTH GRADE June 2010 Billings Public Schools Correlation and Guide Math - McDougal Littell Middle School Math 2004 (Chapter Order: 1, 6, 2, 4, 5, 13, 3, 7, 8, 9, 10, 11, 12 Chapter 1 Number Sense, Patterns,
CALIFORNIA STANDARDS TEST CSM00433 CSM01958 A B C CSM02216 A 583,000
 G R E Which of these is the number 5,005,0? five million, five hundred, fourteen five million, five thousand, fourteen five thousand, five hundred, fourteen five billion, five million, fourteen LIFORNI
G R E Which of these is the number 5,005,0? five million, five hundred, fourteen five million, five thousand, fourteen five thousand, five hundred, fourteen five billion, five million, fourteen LIFORNI
Creating Color Combos
 THE 2016 ROSENTHAL PRIZE for Innovation in Math Teaching Creating Color Combos Visual Modeling of Equivalent Ratios Traci Jackson Lesson Plan Grades 5-6 Table of Contents Creating Color Combos: Visual
THE 2016 ROSENTHAL PRIZE for Innovation in Math Teaching Creating Color Combos Visual Modeling of Equivalent Ratios Traci Jackson Lesson Plan Grades 5-6 Table of Contents Creating Color Combos: Visual
FINAL REVIEW m rounded to the nearest centimeter is _. Choose the correct answer, and write its number in the parentheses.
 FINAL REVIEW Choose the correct answer, and write its number in the parentheses. 1. What is the value of the digit 4 in 135.847? (1) 4 tenths (3) 4 hundredths 4 tens (4) 4 hundreds 2. What is the value
FINAL REVIEW Choose the correct answer, and write its number in the parentheses. 1. What is the value of the digit 4 in 135.847? (1) 4 tenths (3) 4 hundredths 4 tens (4) 4 hundreds 2. What is the value
Jumpstarters for Math
 Jumpstarters for Math Short Daily Warm-ups for the Classroom By CINDY BARDEN COPYRIGHT 2005 Mark Twain Media, Inc. ISBN 10-digit: 1-58037-297-X 13-digit: 978-1-58037-297-8 Printing No. CD-404023 Mark Twain
Jumpstarters for Math Short Daily Warm-ups for the Classroom By CINDY BARDEN COPYRIGHT 2005 Mark Twain Media, Inc. ISBN 10-digit: 1-58037-297-X 13-digit: 978-1-58037-297-8 Printing No. CD-404023 Mark Twain
Unit 7, Lesson 1: Exponent Review
 Unit 7, Lesson 1: Exponent Review Let s review exponents. 1.1: Which One Doesn t Belong: Twos Which expression does not belong? Be prepared to share your reasoning. 8 1.2: Return of the Genie m.openup.org/1/8-7-1-2
Unit 7, Lesson 1: Exponent Review Let s review exponents. 1.1: Which One Doesn t Belong: Twos Which expression does not belong? Be prepared to share your reasoning. 8 1.2: Return of the Genie m.openup.org/1/8-7-1-2
Practice Test. 2. What is the probability of rolling an even number on a number cube? a. 1 6 b. 2 6 c. 1 2 d. 5 be written as a decimal? 3.
 Name: Class: Practice Test. The elevation of the surface of the Dead Sea is -424. meters. In 2005, the height of Mt. Everest was 8,844.4 meters. How much higher was the summit of Mt. Everest? a. -9.268.7
Name: Class: Practice Test. The elevation of the surface of the Dead Sea is -424. meters. In 2005, the height of Mt. Everest was 8,844.4 meters. How much higher was the summit of Mt. Everest? a. -9.268.7
Processes for the Intersection
 7 Timing Processes for the Intersection In Chapter 6, you studied the operation of one intersection approach and determined the value of the vehicle extension time that would extend the green for as long
7 Timing Processes for the Intersection In Chapter 6, you studied the operation of one intersection approach and determined the value of the vehicle extension time that would extend the green for as long
SPEED DRILL WARM-UP ACTIVITY
 SPEED DRILL WARM-UP ACTIVITY Name the operation representative of each of the following: percent left reduction total more half less twice off lower each double Write the equivalents: 20% as a decimal
SPEED DRILL WARM-UP ACTIVITY Name the operation representative of each of the following: percent left reduction total more half less twice off lower each double Write the equivalents: 20% as a decimal
Unit Four Answer Keys
 Multiplication, Division & Fractions Unit Four Unit Four Answer Keys Session Blacklines A.., Unit Four Pre-Assessment Responses will vary. example example a b Sketches will vary. Example: a, Sketches will
Multiplication, Division & Fractions Unit Four Unit Four Answer Keys Session Blacklines A.., Unit Four Pre-Assessment Responses will vary. example example a b Sketches will vary. Example: a, Sketches will
Please fax your students rhythms from p.7 to us AT LEAST THREE DAYS BEFORE the video conference. Our fax number is
 Class Materials 1 Dear Educator, Thank you for choosing the. Inside this packet, you will find all of the materials your class will need for your upcoming Math and Music video conference. There are lessons
Class Materials 1 Dear Educator, Thank you for choosing the. Inside this packet, you will find all of the materials your class will need for your upcoming Math and Music video conference. There are lessons
MITOCW max_min_second_der_512kb-mp4
 MITOCW max_min_second_der_512kb-mp4 PROFESSOR: Hi. Well, I hope you're ready for second derivatives. We don't go higher than that in many problems, but the second derivative is an important-- the derivative
MITOCW max_min_second_der_512kb-mp4 PROFESSOR: Hi. Well, I hope you're ready for second derivatives. We don't go higher than that in many problems, but the second derivative is an important-- the derivative
percents Common Core Standard 7.RP3 Use proportional relationships to solve multistep ratio and percent problems.
 Intro All right, welcome to class everybody I need you guys to come in, take your seat Take out everything you need Put it on top of your desk I have something real special planned for you Now make sure
Intro All right, welcome to class everybody I need you guys to come in, take your seat Take out everything you need Put it on top of your desk I have something real special planned for you Now make sure
Human Number Line. Introduction to Negative Numbers
 Human Number Line Introduction to Negative Numbers 1 WARM UP Plot each number on a number line. Then, insert a. or, symbol to make each inequality statement true. 0 1 2 3 4 5 6 7 8 9 10 1. 3 4 1 1 2 2.
Human Number Line Introduction to Negative Numbers 1 WARM UP Plot each number on a number line. Then, insert a. or, symbol to make each inequality statement true. 0 1 2 3 4 5 6 7 8 9 10 1. 3 4 1 1 2 2.
BPS 7th Grade Pre-Algebra Revised summer 2014 Year at a Glance Unit Standards Practices Days
 BPS 7th Grade Pre-Algebra Revised summer 2014 Year at a Glance Unit Standards Practices Days 1 All Operations with Integers 7.NS.1, 7.NS.2, 7.NS.3 1,4,6,8 7 2 All Operations with Rational Numbers 7.NS.1c,
BPS 7th Grade Pre-Algebra Revised summer 2014 Year at a Glance Unit Standards Practices Days 1 All Operations with Integers 7.NS.1, 7.NS.2, 7.NS.3 1,4,6,8 7 2 All Operations with Rational Numbers 7.NS.1c,
Welcome Accelerated Algebra 2!
 Welcome Accelerated Algebra 2! Tear-Out: Pg. 445-452 (Class notes) Pg. 461 (homework) U6H2: Pg. 390 #21-24 Pg. 448 #6-7, 9-11 Pg. 461 #6-8 Updates: U6Q1 will be February 15 th (Thursday) U6T will be March
Welcome Accelerated Algebra 2! Tear-Out: Pg. 445-452 (Class notes) Pg. 461 (homework) U6H2: Pg. 390 #21-24 Pg. 448 #6-7, 9-11 Pg. 461 #6-8 Updates: U6Q1 will be February 15 th (Thursday) U6T will be March
Encoders and Decoders: Details and Design Issues
 Encoders and Decoders: Details and Design Issues Edward L. Bosworth, Ph.D. TSYS School of Computer Science Columbus State University Columbus, GA 31907 bosworth_edward@colstate.edu Slide 1 of 25 slides
Encoders and Decoders: Details and Design Issues Edward L. Bosworth, Ph.D. TSYS School of Computer Science Columbus State University Columbus, GA 31907 bosworth_edward@colstate.edu Slide 1 of 25 slides
Draft last edited May 13, 2013 by Belinda Robertson
 Draft last edited May 13, 2013 by Belinda Robertson 97 98 Appendix A: Prolem Handouts Problem Title Location or Page number 1 CCA Interpreting Algebraic Expressions Map.mathshell.org high school concept
Draft last edited May 13, 2013 by Belinda Robertson 97 98 Appendix A: Prolem Handouts Problem Title Location or Page number 1 CCA Interpreting Algebraic Expressions Map.mathshell.org high school concept
US_Math 4 1. Operations and Algebraic Thinking 4.OA 2. Number and Operations in Base Ten 4.NBT 3. Number and Operations - Fractions 4.
 US_Math 4 1. Operations and Algebraic Thinking 4.OA 1.1 Multiplication of Whole Numbers 4.OA 1.2 Division of Whole Numbers 4.OA 1.3 Factors and Multiples 4.OA 2. Number and Operations in Base Ten 4.NBT
US_Math 4 1. Operations and Algebraic Thinking 4.OA 1.1 Multiplication of Whole Numbers 4.OA 1.2 Division of Whole Numbers 4.OA 1.3 Factors and Multiples 4.OA 2. Number and Operations in Base Ten 4.NBT
Key Maths Facts to Memorise Question and Answer
 Key Maths Facts to Memorise Question and Answer Ways of using this booklet: 1) Write the questions on cards with the answers on the back and test yourself. 2) Work with a friend to take turns reading a
Key Maths Facts to Memorise Question and Answer Ways of using this booklet: 1) Write the questions on cards with the answers on the back and test yourself. 2) Work with a friend to take turns reading a
Section A Using the n th Term Formula Grade D / C
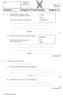 Name: Teacher Assessment Section A Using the n th Term Formula Grade D / C 1. The first term of a sequence is 2. The rule for continuing the sequence is What is the second term of the sequence? Add 7 then
Name: Teacher Assessment Section A Using the n th Term Formula Grade D / C 1. The first term of a sequence is 2. The rule for continuing the sequence is What is the second term of the sequence? Add 7 then
What is Statistics? 13.1 What is Statistics? Statistics
 13.1 What is Statistics? What is Statistics? The collection of all outcomes, responses, measurements, or counts that are of interest. A portion or subset of the population. Statistics Is the science of
13.1 What is Statistics? What is Statistics? The collection of all outcomes, responses, measurements, or counts that are of interest. A portion or subset of the population. Statistics Is the science of
Trimester 2 5 th Grade Name: Answer Key
 Trimester 2 th Grade Name: Answer Key..NBT.7 Fiona hiked along a trail in Glacier National Park that is 7.2 miles long. It took her hours to hike. What was her average speed per hour? 7.2 / =.3 (miles
Trimester 2 th Grade Name: Answer Key..NBT.7 Fiona hiked along a trail in Glacier National Park that is 7.2 miles long. It took her hours to hike. What was her average speed per hour? 7.2 / =.3 (miles
Integer Chips. Explore Mode. In this tool, you can model and solve expressions using integer chips.
 In this tool, you can model and solve expressions using integer chips. Explore Mode 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1. Textbox Add annotations to the activity area. 2. Textbox with Arrow Add comments
In this tool, you can model and solve expressions using integer chips. Explore Mode 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1. Textbox Add annotations to the activity area. 2. Textbox with Arrow Add comments
6 th Grade Semester 2 Review 1) It cost me $18 to make a lamp, but I m selling it for $45. What was the percent of increase in price?
 6 th Grade Semester 2 Review 1) It cost me $18 to make a lamp, but I m selling it for $45. What was the percent of increase in price? 2) Tom's weekly salary changed from $240 to $288. What was the percent
6 th Grade Semester 2 Review 1) It cost me $18 to make a lamp, but I m selling it for $45. What was the percent of increase in price? 2) Tom's weekly salary changed from $240 to $288. What was the percent
Box Plots. So that I can: look at large amount of data in condensed form.
 LESSON 5 Box Plots LEARNING OBJECTIVES Today I am: creating box plots. So that I can: look at large amount of data in condensed form. I ll know I have it when I can: make observations about the data based
LESSON 5 Box Plots LEARNING OBJECTIVES Today I am: creating box plots. So that I can: look at large amount of data in condensed form. I ll know I have it when I can: make observations about the data based
For an alphabet, we can make do with just { s, 0, 1 }, in which for typographic simplicity, s stands for the blank space.
 Problem 1 (A&B 1.1): =================== We get to specify a few things here that are left unstated to begin with. I assume that numbers refers to nonnegative integers. I assume that the input is guaranteed
Problem 1 (A&B 1.1): =================== We get to specify a few things here that are left unstated to begin with. I assume that numbers refers to nonnegative integers. I assume that the input is guaranteed
Q1. In a division sum, the divisor is 4 times the quotient and twice the remainder. If and are respectively the divisor and the dividend, then (a)
 Q1. In a division sum, the divisor is 4 times the quotient and twice the remainder. If and are respectively the divisor and the dividend, then (a) 3 (c) a 1 4b (b) 2 (d) Q2. If is divisible by 11, then
Q1. In a division sum, the divisor is 4 times the quotient and twice the remainder. If and are respectively the divisor and the dividend, then (a) 3 (c) a 1 4b (b) 2 (d) Q2. If is divisible by 11, then
Force & Motion 4-5: ArithMachines
 Force & Motion 4-5: ArithMachines Physical Science Comes Alive: Exploring Things that Go G. Benenson & J. Neujahr City Technology CCNY 212 650 8389 Overview Introduction In ArithMachines students develop
Force & Motion 4-5: ArithMachines Physical Science Comes Alive: Exploring Things that Go G. Benenson & J. Neujahr City Technology CCNY 212 650 8389 Overview Introduction In ArithMachines students develop
Math and Music Developed by Megan Martinez and Alex Barnett in conjunction with Ilene Kanoff
 Math and Music Developed by Megan Martinez and Alex Barnett in conjunction with Ilene Kanoff For questions or comments, feel free to contact Megan Martinez at megan.ann.martinez [at] gmail.com Overview
Math and Music Developed by Megan Martinez and Alex Barnett in conjunction with Ilene Kanoff For questions or comments, feel free to contact Megan Martinez at megan.ann.martinez [at] gmail.com Overview
Uses of Fractions. Fractions
 Uses of The numbers,,,, and are all fractions. A fraction is written with two whole numbers that are separated by a fraction bar. The top number is called the numerator. The bottom number is called the
Uses of The numbers,,,, and are all fractions. A fraction is written with two whole numbers that are separated by a fraction bar. The top number is called the numerator. The bottom number is called the
TL-2900 AMMONIA & NITRATE ANALYZER DUAL CHANNEL
 TL-2900 AMMONIA & NITRATE ANALYZER DUAL CHANNEL DATA ACQUISITION SYSTEM V.15.4 INSTRUCTION MANUAL Timberline Instruments, LLC 1880 S. Flatiron Ct., Unit I Boulder, Colorado 80301 Ph: (303) 440-8779 Fx:
TL-2900 AMMONIA & NITRATE ANALYZER DUAL CHANNEL DATA ACQUISITION SYSTEM V.15.4 INSTRUCTION MANUAL Timberline Instruments, LLC 1880 S. Flatiron Ct., Unit I Boulder, Colorado 80301 Ph: (303) 440-8779 Fx:
Switching Circuits & Logic Design, Fall Final Examination (1/13/2012, 3:30pm~5:20pm)
 Switching Circuits & Logic Design, Fall 2011 Final Examination (1/13/2012, 3:30pm~5:20pm) Problem 1: (15 points) Consider a new FF with three inputs, S, R, and T. No more than one of these inputs can be
Switching Circuits & Logic Design, Fall 2011 Final Examination (1/13/2012, 3:30pm~5:20pm) Problem 1: (15 points) Consider a new FF with three inputs, S, R, and T. No more than one of these inputs can be
1-1 Variables and Expressions
 1-1 Variables and Expressions Warm Up Lesson Presentation Lesson Quiz Warm Up Add or subtract. 1. 6 + 104 110 2. 12(9) 108 3. 23 8 15 4. Multiply or divide. 5. 324 18 18 6. 6 7. 13.5(10) 135 8. 18.2 2
1-1 Variables and Expressions Warm Up Lesson Presentation Lesson Quiz Warm Up Add or subtract. 1. 6 + 104 110 2. 12(9) 108 3. 23 8 15 4. Multiply or divide. 5. 324 18 18 6. 6 7. 13.5(10) 135 8. 18.2 2
MATH& 146 Lesson 11. Section 1.6 Categorical Data
 MATH& 146 Lesson 11 Section 1.6 Categorical Data 1 Frequency The first step to organizing categorical data is to count the number of data values there are in each category of interest. We can organize
MATH& 146 Lesson 11 Section 1.6 Categorical Data 1 Frequency The first step to organizing categorical data is to count the number of data values there are in each category of interest. We can organize
amount base = percent 30% of the class 90% of the points 65% of the televisions
 Free Pre-Algebra Lesson 41! page 1 Lesson 41 Solving Percent Equations A percent is really a ratio, usually of part to whole. In percent problems, the numerator of the ratio (the part) is called the, and
Free Pre-Algebra Lesson 41! page 1 Lesson 41 Solving Percent Equations A percent is really a ratio, usually of part to whole. In percent problems, the numerator of the ratio (the part) is called the, and
Lesson 5: Events and Venn Diagrams
 Lesson 5: Events and Venn Diagrams DO NOW: Shading Regions of a Venn Diagram At a high school, some students play soccer, and some do not. Also, some students play basketball, and some do not. This scenario
Lesson 5: Events and Venn Diagrams DO NOW: Shading Regions of a Venn Diagram At a high school, some students play soccer, and some do not. Also, some students play basketball, and some do not. This scenario
DATA COMPRESSION USING THE FFT
 EEE 407/591 PROJECT DUE: NOVEMBER 21, 2001 DATA COMPRESSION USING THE FFT INSTRUCTOR: DR. ANDREAS SPANIAS TEAM MEMBERS: IMTIAZ NIZAMI - 993 21 6600 HASSAN MANSOOR - 993 69 3137 Contents TECHNICAL BACKGROUND...
EEE 407/591 PROJECT DUE: NOVEMBER 21, 2001 DATA COMPRESSION USING THE FFT INSTRUCTOR: DR. ANDREAS SPANIAS TEAM MEMBERS: IMTIAZ NIZAMI - 993 21 6600 HASSAN MANSOOR - 993 69 3137 Contents TECHNICAL BACKGROUND...
COSC3213W04 Exercise Set 2 - Solutions
 COSC313W04 Exercise Set - Solutions Encoding 1. Encode the bit-pattern 1010000101 using the following digital encoding schemes. Be sure to write down any assumptions you need to make: a. NRZ-I Need to
COSC313W04 Exercise Set - Solutions Encoding 1. Encode the bit-pattern 1010000101 using the following digital encoding schemes. Be sure to write down any assumptions you need to make: a. NRZ-I Need to
MIT Alumni Books Podcast The Proof and the Pudding
 MIT Alumni Books Podcast The Proof and the Pudding JOE This is the MIT Alumni Books Podcast. I'm Joe McGonegal, Director of Alumni Education. My guest, Jim Henle, Ph.D. '76, is the Myra M. Sampson Professor
MIT Alumni Books Podcast The Proof and the Pudding JOE This is the MIT Alumni Books Podcast. I'm Joe McGonegal, Director of Alumni Education. My guest, Jim Henle, Ph.D. '76, is the Myra M. Sampson Professor
On Your Own. Applications. Unit 2. ii. The following are the pairs of mutual friends: A-C, A-E, B-D, C-D, and D-E.
 Applications 1 a. i. No, students A and D are not mutual friends because D does not consider A a friend. ii. The following are the pairs of mutual friends: A-C, A-E, B-D, C-D, and D-E. iii. Each person
Applications 1 a. i. No, students A and D are not mutual friends because D does not consider A a friend. ii. The following are the pairs of mutual friends: A-C, A-E, B-D, C-D, and D-E. iii. Each person
Eagle Business Software
 Rental Table of Contents Introduction... 1 Technical Support... 1 Overview... 2 Getting Started... 5 Inventory Folders for Rental Items... 5 Rental Service Folders... 5 Equipment Inventory Folders...
Rental Table of Contents Introduction... 1 Technical Support... 1 Overview... 2 Getting Started... 5 Inventory Folders for Rental Items... 5 Rental Service Folders... 5 Equipment Inventory Folders...
Pitch correction on the human voice
 University of Arkansas, Fayetteville ScholarWorks@UARK Computer Science and Computer Engineering Undergraduate Honors Theses Computer Science and Computer Engineering 5-2008 Pitch correction on the human
University of Arkansas, Fayetteville ScholarWorks@UARK Computer Science and Computer Engineering Undergraduate Honors Theses Computer Science and Computer Engineering 5-2008 Pitch correction on the human
Berkeley City College Intermediate Algebra - Math Ch 3
 Berkeley City College Intermediate Algebra - Math 203 - Ch 3 Homework Problems Due Date: Name To receive full credit for the assignment you must attach extra sheets of paper to the packet and show your
Berkeley City College Intermediate Algebra - Math 203 - Ch 3 Homework Problems Due Date: Name To receive full credit for the assignment you must attach extra sheets of paper to the packet and show your
Chapter 7 Probability
 Chapter 7 Probability Copyright 2006 Brooks/Cole, a division of Thomson Learning, Inc. 7.1 Random Circumstances Random circumstance is one in which the outcome is unpredictable. Case Study 1.1 Alicia Has
Chapter 7 Probability Copyright 2006 Brooks/Cole, a division of Thomson Learning, Inc. 7.1 Random Circumstances Random circumstance is one in which the outcome is unpredictable. Case Study 1.1 Alicia Has
Centre for Economic Policy Research
 The Australian National University Centre for Economic Policy Research DISCUSSION PAPER The Reliability of Matches in the 2002-2004 Vietnam Household Living Standards Survey Panel Brian McCaig DISCUSSION
The Australian National University Centre for Economic Policy Research DISCUSSION PAPER The Reliability of Matches in the 2002-2004 Vietnam Household Living Standards Survey Panel Brian McCaig DISCUSSION
2.2. Multiplying and Dividing Powers. INVESTIGATE the Math
 . Multipling and Dividing Powers GOAL Develop and appl exponent principles to multipl and divide powers. INVESTIGATE the Math Amir thought there was a wa to simplif 1 6 1 9 1 without using a calculator.?
. Multipling and Dividing Powers GOAL Develop and appl exponent principles to multipl and divide powers. INVESTIGATE the Math Amir thought there was a wa to simplif 1 6 1 9 1 without using a calculator.?
Short Questions 1. BMW. 2. Jetta. 3. Volvo. 4. Corvette. 5. Cadillac
 Short Questions 1. Consider the following 5 cars plotted in the following graph. Suppose that these cars are fully described by their spaciousness and acceleration, i.e., there are no other characteristics
Short Questions 1. Consider the following 5 cars plotted in the following graph. Suppose that these cars are fully described by their spaciousness and acceleration, i.e., there are no other characteristics
Unit 7 : Chap. 1 Inductive and Deductive Reasoning
 Unit 7 : Chap. 1 Inductive and Deductive Reasoning Inductive Reasoning: Involves making conjectures based on patterns or observations. Conjectures are much like hypothesis in science. Ex. ) Today it is
Unit 7 : Chap. 1 Inductive and Deductive Reasoning Inductive Reasoning: Involves making conjectures based on patterns or observations. Conjectures are much like hypothesis in science. Ex. ) Today it is
Lab P-6: Synthesis of Sinusoidal Signals A Music Illusion. A k cos.! k t C k / (1)
 DSP First, 2e Signal Processing First Lab P-6: Synthesis of Sinusoidal Signals A Music Illusion Pre-Lab: Read the Pre-Lab and do all the exercises in the Pre-Lab section prior to attending lab. Verification:
DSP First, 2e Signal Processing First Lab P-6: Synthesis of Sinusoidal Signals A Music Illusion Pre-Lab: Read the Pre-Lab and do all the exercises in the Pre-Lab section prior to attending lab. Verification:
School: Phone: Principal:
 Third Grade Report Card District: Hillsboro School District 1J Student Name: Academic Year: 2014-2015 Teacher: School: Phone: Principal: ATTENDANCE To The Parents/Guardians Of: Reporting Period QT1 SM1
Third Grade Report Card District: Hillsboro School District 1J Student Name: Academic Year: 2014-2015 Teacher: School: Phone: Principal: ATTENDANCE To The Parents/Guardians Of: Reporting Period QT1 SM1
Rental Setup and Serialized Rentals
 MBS ARC (Textbook) Manual Rental Setup and Serialized Rentals Setups for rentals include establishing defaults for the following: Coding rental refunds and writeoffs. Rental letters. Creation of secured
MBS ARC (Textbook) Manual Rental Setup and Serialized Rentals Setups for rentals include establishing defaults for the following: Coding rental refunds and writeoffs. Rental letters. Creation of secured
THE OPERATION OF A CATHODE RAY TUBE
 THE OPERATION OF A CATHODE RAY TUBE OBJECT: To acquaint the student with the operation of a cathode ray tube, and to study the effect of varying potential differences on accelerated electrons. THEORY:
THE OPERATION OF A CATHODE RAY TUBE OBJECT: To acquaint the student with the operation of a cathode ray tube, and to study the effect of varying potential differences on accelerated electrons. THEORY:
Fixed-Point Calculator
 Fixed-Point Calculator Robert Kozubiak, Muris Zecevic, Cameron Renny Electrical and Computer Engineering Department School of Engineering and Computer Science Oakland University, Rochester, MI rjkozubiak@oakland.edu,
Fixed-Point Calculator Robert Kozubiak, Muris Zecevic, Cameron Renny Electrical and Computer Engineering Department School of Engineering and Computer Science Oakland University, Rochester, MI rjkozubiak@oakland.edu,
Name Of The Experiment: Sequential circuit design Latch, Flip-flop and Registers
 EEE 304 Experiment No. 07 Name Of The Experiment: Sequential circuit design Latch, Flip-flop and Registers Important: Submit your Prelab at the beginning of the lab. Prelab 1: Construct a S-R Latch and
EEE 304 Experiment No. 07 Name Of The Experiment: Sequential circuit design Latch, Flip-flop and Registers Important: Submit your Prelab at the beginning of the lab. Prelab 1: Construct a S-R Latch and
Math Released Item Grade 5. Whole Number and Fraction Part 0542-M02399
 Math Released Item 2017 Grade 5 Whole Number and Fraction Part 0542-M02399 Anchor Set A1 A10 With Annotations Prompt 0542-M02399 - Rubric Part A Score Description Student response includes the following
Math Released Item 2017 Grade 5 Whole Number and Fraction Part 0542-M02399 Anchor Set A1 A10 With Annotations Prompt 0542-M02399 - Rubric Part A Score Description Student response includes the following
Unit 07 PC Form A. 1. Use pencil and paper to answer the question. Plot and label each point on the coordinate grid.
 1. Use pencil and paper to answer the question. Plot and label each point on the coordinate grid. A (5,2) B (2,2) C (0,0) D (1,3) E (2,4) 2. Use pencil and paper to answer the question. Write two fractions
1. Use pencil and paper to answer the question. Plot and label each point on the coordinate grid. A (5,2) B (2,2) C (0,0) D (1,3) E (2,4) 2. Use pencil and paper to answer the question. Write two fractions
The reduction in the number of flip-flops in a sequential circuit is referred to as the state-reduction problem.
 State Reduction The reduction in the number of flip-flops in a sequential circuit is referred to as the state-reduction problem. State-reduction algorithms are concerned with procedures for reducing the
State Reduction The reduction in the number of flip-flops in a sequential circuit is referred to as the state-reduction problem. State-reduction algorithms are concerned with procedures for reducing the
McRuffy Press Fourth Grade Color Math Test 7
 McRuffy Press Fourth Grade Color Math Test 7 Materials: Test pages (Resource pack, 3 sheets) Test Directions Page :. Problem solving: Solve the problems. 2. Fractions to decimals: Change the fractions
McRuffy Press Fourth Grade Color Math Test 7 Materials: Test pages (Resource pack, 3 sheets) Test Directions Page :. Problem solving: Solve the problems. 2. Fractions to decimals: Change the fractions
Math: Fractions and Decimals 105
 Math: Fractions and Decimals 105 Many students face fractions with trepidation; they re too hard, I don t understand. If this is you, there is no better tool to bring yourself back up to speed than a tape
Math: Fractions and Decimals 105 Many students face fractions with trepidation; they re too hard, I don t understand. If this is you, there is no better tool to bring yourself back up to speed than a tape
MATHEMATICAL THINKING
 MATHEMATICAL THINKING Numbers and their Algebra James Tanton (with additional tidbits by Kit Norris) COMMENT: These notes are based on content from the THINKING MATHEMATICS! Volume 1: Arithmetic = Gateway
MATHEMATICAL THINKING Numbers and their Algebra James Tanton (with additional tidbits by Kit Norris) COMMENT: These notes are based on content from the THINKING MATHEMATICS! Volume 1: Arithmetic = Gateway
Lab experience 1: Introduction to LabView
 Lab experience 1: Introduction to LabView LabView is software for the real-time acquisition, processing and visualization of measured data. A LabView program is called a Virtual Instrument (VI) because
Lab experience 1: Introduction to LabView LabView is software for the real-time acquisition, processing and visualization of measured data. A LabView program is called a Virtual Instrument (VI) because
I) Documenting Rhythm The Time Signature
 the STARTING LINE I) Documenting Rhythm The Time Signature Up to this point we ve been concentrating on what the basic aspects of drum literature looks like and what they mean. To do that we started by
the STARTING LINE I) Documenting Rhythm The Time Signature Up to this point we ve been concentrating on what the basic aspects of drum literature looks like and what they mean. To do that we started by
x) Graph the function
 1) If and, find and 2) If, find 3) Use the definition of logarithms to rewrite this equation in exponential form: 4) Expand 5) a) Evaluate and show how you got the answer without a calculator. b) Evaluate
1) If and, find and 2) If, find 3) Use the definition of logarithms to rewrite this equation in exponential form: 4) Expand 5) a) Evaluate and show how you got the answer without a calculator. b) Evaluate
Printed Documentation
 Printed Documentation Table of Contents INTRODUCTION... 1 Technical Support... 1 Overview... 2 GETTING STARTED... 3 Inventory Folders for Rental Items... 3 Rental Service Folders... 4 Equipment Inventory
Printed Documentation Table of Contents INTRODUCTION... 1 Technical Support... 1 Overview... 2 GETTING STARTED... 3 Inventory Folders for Rental Items... 3 Rental Service Folders... 4 Equipment Inventory
