Euler s Art of Reckoning 1
|
|
|
- Simon Williamson
- 6 years ago
- Views:
Transcription
1 Euler s Art of Reckoning 1 Christian Siebeneicher 2 Abstract: The Art of Reckoning has always been part of human culture, but to my knowledge there have been only two eminent mathematicians who wrote a book on the subject: Leonardo of Pisa in 1202 and Leonhard Euler in 1738 (for schools in St. Petersburg). While Fibonacci assumes some prior familiarity with it, Euler develops it from its beginning in a timelessly clear fashion. In his preface he expresses his conviction that learning is without value as long as it does not lead to understanding. I think that even today his book can serve as a guide for anyone who wishes to teach arithmetic to children. In my talk I will pay particular attention to the kind of problems used in Liping Ma s survey. During the last four years, I have been involved in the math education of future elementary school teachers, and for much of that time, I was searching for a book in which elementary arithmetic would be developed from scratch in a manner understandable to T. C. Mits 3. When by chance I came across Euler s Einleitung zur Rechenkunst, I immediately realized that I found it. Euler s book contains all the arithmetic that in my opinion every elementary school teacher should have learned 4. I think that Liping Ma s findings, published in her book Knowing and Teaching Elementary Mathematics : Teachers Understanding of Fundamental Mathematics in China and the United States, confirm that view. To illustrate my conviction I shall juxtapose the first two questions from Liping Ma s book with corresponding parts of Euler s Einleitung zur Rechenkunst. To a German audience I could directly present Euler s words. They sound a bit old fashioned and long winded to modern ears, but they would force the reader to read slowly. Thereby the reader would discover that every word is chosen carefully and would also find that an adaption of Euler s language to modern German would not be easy. An adequate translation into English is even less so. My friend Klaus Hoechsmann took on the demanding job of translating those parts of Euler s book which I want to use in this talk. I think that he did it in a way which preserved Euler s intentions, and I thank him for his invaluable help. I am indebted to him in another respect. When I started my job as mathematics educator for primary school teachers four years ago, I rarely used a 1 Leonhard Euler, Einleitung zur Rechenkunst, Opera Omnia, Ser. III, Vol. 2 2 Universität Bielefeld, Fakultät für Mathematik, D Bielefeld, Germany 3 T. C. Mits := The Celebrated Man In The Street. Lillian R. Lieber and Hugh Gray Lieber, The education of T. C. Mits. 4 Please forget what you have learned in school; you havent t learned it. Edmund Landau in the Preface for the Student in his Grundlagen der Analysis. 1
2 pocket calculator. At that time long before I came to know Euler s Art of Reckoning he showed me how to extend the range of a pocket calculator beyond its natural bounds. This will be used in example at the end of my talk. Subtraction With Regrouping: Approaches To Teaching A Topic Scenario Let s spend some time thinking about one particular topic that you may work with when you teach subtraction with regrouping. Look at these questions How would you approach these problems if you were teaching second grade? What would you say pupils would need to understand or be able to do before they could start learning subtraction with regrouping? etc. Reading Euler Rule But if the pieces of a certain value are more abundant in the second number than in the first one so that subtraction cannot succeed in the manner described then one piece of the next higher value must be removed from the first number and changed into 10 pieces of the lower value, thus making subtraction possible. For the next step in the subtraction, however, it must be remembered that the first number has been diminished by one. Reason Just as in an addition, when there are more than 9 pieces of a certain value, and ten of them are removed and changed into one piece of the next higher value, so but in reverse it happens in subtraction: when not enough pieces of one value are available in the first number to allow subtracting the amount required by the second number, one piece of the next higher value is taken off, yielding 10 of the previous type, and those ten are put in with the rest. For, if from a number one Hundred, say, is taken away but 10 Tens are added in again, the size of number does not change. Consequently a change of this sort may surely be used to facilitate subtraction. 2
3 Multidigit Number Multiplication: Dealing With Students Mistakes Scenario Some sixth grade teachers noticed that several of their students were making the same mistake in multiplying large numbers. In trying to calculate the students seemed to be forgetting to move the numbers (i.e., the partial products) over on each line. They were doing this: instead of this: While these teachers agreed that this was a problem, they did not agree on what to do about it. What would you do if you were teaching sixth grade and you noticed that several of your students were doing this? Reading Euler Rule If a number, however large it may be, is to be multiplied by 10, one only needs to append a zero to the right of it. If a number is to be multiplied by 100, one has to append two zeroes. To multiply by 1000 one appends three zeroes,... and so on, always as many zeroes as follow the 1 in the multiplier. Explanation If a number is to be multiplied by 10 then every part of that number must be multiplied by 10. Multiplying the Units by 10 yields as many Tens as there were Units. The Tens, however, are changed into Hundreds, the Hundreds into Thousands,... and so on. Since, by appending a 0 to the right of a given number, every value is changed into the next higher one which is ten times greater it makes the entire number ten times greater. Consequently 10 times 5783 is as much as
4 Likewise, if two zeroes are appended to the right of a number the Units become Hundreds, the Tens become Thousands, the Hundreds become Tenthousands and so on; every value is changed into another, which is 100 times greater. Hence by appending two zeroes, the entire number is multiplied by 100. Thus, when 328 is multiplied by 100, one obtains In a similar way one sees that, if three zeroes are appended to a number it becomes 1000 times bigger, and so forth. If, for example, 5430 is multiplied by , the product will be In this way, one sees how to multiply any number by a number written as a 1 followed by a string of zeroes. And this is the basis of all rules for multiplication by large composite numbers, as will be further explained below. Rule If the multiplier that is, the number by which a given number is to be multiplied is a simple number followed by a string of zeros, such as 60, 300, 4000, etc., then one finds the product by multiplying first with the simple number and then appending to the right hand as many zeros as are in the multiplier. Explanation Fundamental Rule If the multiplier for a given number is itself the result of multiplying two numbers, one obtains the true product by first multiplying the given number by one of these two numbers and then multiplying this product by the other number. Explanation of the Fundamental Rule When I am to multiply 47 with 6 because 6 is as much as 2 times 3 I find the product by multiplying first with 2, which makes 94, and then multiplying those 94 with 3, which gives 282; and that is the number which results when 47 is multiplied by 6. Because 6 is 2 times 3, the product to be determined namely 6 times 47 is the same as 2 times 3 times 47 or 3 times 2 times 47. To find what 3 times 2 times 47 is, one first finds 2 times 47, which is 94. Therefore 3 times 2 times 47 is 3 times 94, and consequently 3 times 94 is the same as 6 times 47. This shows the reason for the fundamental rule which is equally valid in all possible cases. By the fundamental rule, many multiplications can be performed even if the multiplier is not a simple number 5. So, for example if 127 is to be multiplied by 63, then since 63 is the same as 7 times 9, one may first multiply the 5 The fundamental rule is one of the ingredients for daily life calculations outside the standard schemes. It is known that Gauss was inclined to this type of reckoning. See: C. F. Gauss, Werke X 2, P. Maennchen, Gauss als Zahlenrechner and C. F. Gauss Disquisitiones Arithmeticae, Part Six. 4
5 number 127 by 7, getting 889. Thereafter multiplication of 889 by 9 gives 8001, and this is as many as 63 times 127. Since 8001 is 9 times 889, and since 889 is 7 times 127, it follows that 8001 is 9 times 7 times 127. But 9 times 7 ist 63, and therefore 8001 is 63 times 127. This example clarifies truth of the fundamental rule even further. To arrive at the proposed rule itself, however, it is to be noted that a simple number with a string of trailing zeroes results from multiplying that simple number by a 1 with as many zeros attached. Therefore, to multiply by such a number, one can first multiply by the simple number, and the resulting product by a 1 with as many zeroes attached. It has already been shown that this can be done by simply appending that many zeroes. So, if the multiplier is a single digit with a string of trailing zeroes, one multiplies first with the simple number and then appends to the product as many zeroes as the multiplier has to the right of its first digit. If, for instance, 543 is to be multiplied by 700 one first multiplies 543 by 7, which is 3801, and with two appended zeroes gives and that is the desired product, namely 700 times 543. Since multiplication by a simple number is carried out from right to left, one may immediatly write down on the right as many zeros as there are in the multiplier and then carry out the multiplication by the simple number. In this manner the operation in the preceeding example is done as follows: 543 number 700 multiplier product Rule If the multiplier is a number with many digits, the given number must be multiplied by every part of the multiplier, and all these products must be added, since the resulting sum will be the desired product. Reason We have already shown that if the given number is composed of several parts, then every part must be multiplied by the multiplier and all these particular products be put together, as their sum will give the desired product. But since the two factors may be interchanged, this also applies to the multiplier. Therefore if the latter has several digits, the given number must be multiplied by each part, and all these individual products must be added: because their sum gives the desired product. 5
6 The parts of a multidigit number, however, are the different value groups, such as Units, Tens, Hundreds, etc., each containing no more than 9 pieces. Therefore the given number must be multiplied first by as many Units as there are in the multiplier, then with as many Tens and similarly with as many Hundreds, and so on as there are in the multiplier, and all the products obtained in this way must be put into a sum. It has already been shown how to multiply by a simple number with a string of trailing zeroes, and the various parts of the multiplier are numbers of precisely this type whence multiplication with such a compound or multidigit multiplier will cause no difficulties. If for example one has to multiply 4738 with 358 then the parts of the multiplicator are firstly 8, then 50 and thirdly 300. Because of this one multiplies the number 4738 first with 8, which gives Then one multiplies the number 4738 with 50, getting Thirdly one multiplies the given number with 300, and this yields These three products have to be added as follows: and the sum is the demanded product In order to make the whole operation more comfortable one writes the resulting products under each other in such a manner that Units come under Units and all the like value types are placed under each other, so that addition can be carried out immediately as follows: 4738 number 358 multiplier product One first writes the multiplier under the number to be multiplied, and traces a line under them. 6
7 After this one multiplies the number by as many units as there are in the multiplier, namely 8, and writes the product under the line as been taught in the multiplication with simple numbers. Then one multiplies with the Tens of the multiplier, i.e., by 50, writing according to the rule given above into the place of the Units a zero, and then simply multiplying by 5. Thirdly one multiplies with the Hundreds, in this case by 300, writing into the first two places from the right two zeroes, and then simply multiplying by 3. If one writes the digits properly under each other, then, in the resulting products, the different value types are placed under each other, making addition much easier. After one has found all the particular products, a line is drawn under them and they are added together, thus yielding the required product. One may for the sake of brevity leave out the zeroes which had to be written on the right for the higher value types, because they contribute nothing to the addition, as follows: Here it may be noted that the product for each digit of the multiplier starts from the right exactly where this digit is placed. So, the product with the first digit from the right of the multiplier starts from the first place. The product with the second digit starts in the second place, that with the third in the third place, and so on. An Application In the preface to his book Euler says: Since learning the art of reckoning without some basis in reason is neither sufficient for treating all possible cases nor apt to sharpen the mind as should be our special intent so we have striven, in the present guide, to expound and explain the reasons for all rules and operations in such a way that even persons who are not yet skilled in thourough discussion can see and understand them; nonetheless, the rules and shortcuts appropriate to 7
8 calculation were described in detail and extensively clarified by examples. By this device, we hope that young people, besides acquiring an adequate proficiency in calculation, will always be aware of the true reason behind every operation, and in this way gradually become accustomed to thorough reflection. For, when they thus not only grasp the rules, but also clearly see their basis and origin, they will in some measure be enabled to invent new rules of their own, and, by means of these, solve problems for which the ordinary rules are insufficient. A Babylonian clay tablet from the Seleucid period contains the following sequence of numbers: :4 2:8 4:16 8:32. The tablet contains also the remark that the sum of these numbers is 17:3. Evidently the first six numbers are terms of the doubling sequence. Appending the word seconds to these numbers suggests to continue after 32 seconds with 1 minute and 4 seconds, 2 minutes and 8 seconds and so on. This shows that the numbers on the tablet consist of subsequent terms of the doubling sequence. Hence the sum of these numbers must be 17:3, as remarked. The sum of the first 64 terms of the doubling sequence well known as the number of wheat grains on the chess board appears in Al Birunis Chronology ( 1000 A.D.) in decimal and in Babylonian writing: :30:27:9:5:3:50:40:31:0:15. Question: Do these two strings of digits represent the same number? Al Biruni used the pattern of the chess board to structure his computation: 1. Onto the 8 fields of first line of the board he put the numbers 1 2 = = = = = = = 2 7 with sum 255 = (of course not in this notation, which was introduced more than six centuries later by Viète and Descartes). 2. Then he proceeded by squaring 2 8 = 256 and arrived at (2 8 ) 2 = 2 16 = 65536, which is one more than the sum of the numbers placed onto the 16 fields of the first two lines, 3. then again by squaring he arrived at (2 16 ) 2 = 2 32 = , which is one more than the sum of the numbers placed onto the 32 fields of the first four lines, 8
9 4. and finally again by squaring he arrived at (2 32 ) 2 = 2 64 = , and that is one more than the sum of all the numbers placed onto the 64 fields of the chess board. At that time of course the calculation had to be carried out by hand. Today one would prefer the use a pocket calculator for a calculation of this type. If the calculator displays 10 digits, the first three steps above are executed simply by pushing buttons. But squaring 2 32 leads to e+19 and that poses a problem for the determination of the precise number of wheat grains on the board: we all know that subtracting 1 from a number decreases that number. But pushing buttons 1 and does not change the display of the calculator at all. So the modern tool for calculation seems to be useless to determine the precise value of the sum of all the numbers placed on the chess board! One more time: Reading Euler The characters used to describe numbers are arbitrary: every manner to express the numbers has its particular rules for the arithmetic operations. These rules have to be derived from the properties of the pieces of different value. Therefore since the pocket calculator displays the product of two five digit numbers correctly it seems natural to change the system of numeration in a way which takes this into account. So we now use Five digit numbers or Hands of digits as the units. Then Euler s remarks for the multiplication of multidigit numbers may be carried over to the present situation and the process of squaring takes the following form: Subtracting one from the result supplies the desired sum. Fibonacci in his Liber Abbaci went one step further and asked for the sum of all the numbers of the doubling sequence placed onto two adjacent chessboards. This number is obtained of course by squaring
10 and subtracting 1 from the result. The Liber Abbaci contains the following result: Exercise: One of the 8 s in Fibonacci s result is wrong. Which one is it and by what does it have to be replaced? Final Remark I think that even today there is no better introduction to elementary arithmetic than Euler s Einleitung zur Rechenkunst. Therefore the recommendation which Laplace gave to his students, as well as the words of Gauss, Lisez Euler, c est notre maître à tous 6 Das Studium der Werke Euler s bleibt die beste Schule in den verschiedenen Gebieten der Mathematik und kann durch nichts ersetzt werden 7 are as relevant today as they were two hundred years ago. Therefore: Lisez Euler Read Euler! 6 Read Euler. He is the master of us all. 7 Studying Euler s works remains the best school for the different areas of mathematics and can be replaced by nothing else. 10
The Product of Two Negative Numbers 1
 1. The Story 1.1 Plus and minus as locations The Product of Two Negative Numbers 1 K. P. Mohanan 2 nd March 2009 When my daughter Ammu was seven years old, I introduced her to the concept of negative numbers
1. The Story 1.1 Plus and minus as locations The Product of Two Negative Numbers 1 K. P. Mohanan 2 nd March 2009 When my daughter Ammu was seven years old, I introduced her to the concept of negative numbers
Scientific Notation and Significant Figures CH 2000: Introduction to General Chemistry, Plymouth State University SCIENTIFIC NOTATION
 Scientific Notation and Significant Figures CH 2000: Introduction to General Chemistry, Plymouth State University SCIENTIFIC NOTATION I. INTRODUCTION In science, especially in chemistry, it is common to
Scientific Notation and Significant Figures CH 2000: Introduction to General Chemistry, Plymouth State University SCIENTIFIC NOTATION I. INTRODUCTION In science, especially in chemistry, it is common to
An Introduction to Egyptian Mathematics
 An Introduction to Mathematics Some of the oldest writing in the world is on a form of paper made from papyrus reeds that grew all along the Nile river in Egypt. The reeds were squashed and pressed into
An Introduction to Mathematics Some of the oldest writing in the world is on a form of paper made from papyrus reeds that grew all along the Nile river in Egypt. The reeds were squashed and pressed into
Math Released Item Grade 5. Whole Number and Fraction Part 0542-M02399
 Math Released Item 2017 Grade 5 Whole Number and Fraction Part 0542-M02399 Anchor Set A1 A10 With Annotations Prompt 0542-M02399 - Rubric Part A Score Description Student response includes the following
Math Released Item 2017 Grade 5 Whole Number and Fraction Part 0542-M02399 Anchor Set A1 A10 With Annotations Prompt 0542-M02399 - Rubric Part A Score Description Student response includes the following
DIFFERENTIATE SOMETHING AT THE VERY BEGINNING THE COURSE I'LL ADD YOU QUESTIONS USING THEM. BUT PARTICULAR QUESTIONS AS YOU'LL SEE
 1 MATH 16A LECTURE. OCTOBER 28, 2008. PROFESSOR: SO LET ME START WITH SOMETHING I'M SURE YOU ALL WANT TO HEAR ABOUT WHICH IS THE MIDTERM. THE NEXT MIDTERM. IT'S COMING UP, NOT THIS WEEK BUT THE NEXT WEEK.
1 MATH 16A LECTURE. OCTOBER 28, 2008. PROFESSOR: SO LET ME START WITH SOMETHING I'M SURE YOU ALL WANT TO HEAR ABOUT WHICH IS THE MIDTERM. THE NEXT MIDTERM. IT'S COMING UP, NOT THIS WEEK BUT THE NEXT WEEK.
WJEC MATHEMATICS INTERMEDIATE ALGEBRA. SEQUENCES & Nth TERM
 WJEC MATHEMATICS INTERMEDIATE ALGEBRA SEQUENCES & Nth TERM 1 Contents Number Machines Continuing a sequence Finding the nth term Writing terms using the nth term Picture Sequences Credits WJEC Question
WJEC MATHEMATICS INTERMEDIATE ALGEBRA SEQUENCES & Nth TERM 1 Contents Number Machines Continuing a sequence Finding the nth term Writing terms using the nth term Picture Sequences Credits WJEC Question
Bite Size Brownies. Designed by: Jonathan Thompson George Mason University, COMPLETE Math
 Bite Size Brownies Designed by: Jonathan Thompson George Mason University, COMPLETE Math The Task Mr. Brown E. Pan recently opened a new business making brownies called The Brown E. Pan. On his first day
Bite Size Brownies Designed by: Jonathan Thompson George Mason University, COMPLETE Math The Task Mr. Brown E. Pan recently opened a new business making brownies called The Brown E. Pan. On his first day
Here s a question for you: What happens if we try to go the other way? For instance:
 Prime Numbers It s pretty simple to multiply two numbers and get another number. Here s a question for you: What happens if we try to go the other way? For instance: With a little thinking remembering
Prime Numbers It s pretty simple to multiply two numbers and get another number. Here s a question for you: What happens if we try to go the other way? For instance: With a little thinking remembering
1/ 19 2/17 3/23 4/23 5/18 Total/100. Please do not write in the spaces above.
 1/ 19 2/17 3/23 4/23 5/18 Total/100 Please do not write in the spaces above. Directions: You have 50 minutes in which to complete this exam. Please make sure that you read through this entire exam before
1/ 19 2/17 3/23 4/23 5/18 Total/100 Please do not write in the spaces above. Directions: You have 50 minutes in which to complete this exam. Please make sure that you read through this entire exam before
Writing maths, from Euclid to today
 Writing maths, from Euclid to today ONE: EUCLID The first maths book of all time, and the maths book for most of the last 2300 years, was Euclid s Elements. Here the bit from it on Pythagoras s Theorem.
Writing maths, from Euclid to today ONE: EUCLID The first maths book of all time, and the maths book for most of the last 2300 years, was Euclid s Elements. Here the bit from it on Pythagoras s Theorem.
History of Math for the Liberal Arts CHAPTER 3. Babylonian Mathematics. Lawrence Morales. Seattle Central Community College
 1 3 4 5 6 History of Math for the Liberal Arts 7 8 9 CHAPTER 3 10 11 1 13 14 15 16 17 Babylonian Mathematics Lawrence Morales 18 19 0 Seattle Central Community College MAT107 Chapter 3, Lawrence Morales,
1 3 4 5 6 History of Math for the Liberal Arts 7 8 9 CHAPTER 3 10 11 1 13 14 15 16 17 Babylonian Mathematics Lawrence Morales 18 19 0 Seattle Central Community College MAT107 Chapter 3, Lawrence Morales,
Rubato: Towards the Gamification of Music Pedagogy for Learning Outside of the Classroom
 Rubato: Towards the Gamification of Music Pedagogy for Learning Outside of the Classroom Peter Washington Rice University Houston, TX 77005, USA peterwashington@alumni.rice.edu Permission to make digital
Rubato: Towards the Gamification of Music Pedagogy for Learning Outside of the Classroom Peter Washington Rice University Houston, TX 77005, USA peterwashington@alumni.rice.edu Permission to make digital
Correlation to the Common Core State Standards
 Correlation to the Common Core State Standards Go Math! 2011 Grade 4 Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Correlation to the Common Core State Standards Go Math! 2011 Grade 4 Common Core is a trademark of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
The Number Devil: A Mathematical Adventure -By Hans Magnus Enzensberger 2 nd 9 wks Honors Math Journal Project Mrs. C. Thompson's Math Class
 The Number Devil: A Mathematical Adventure -By Hans Magnus Enzensberger 2 nd 9 wks Honors Math Journal Project Mrs. C. Thompson's Math Class DUE: Tuesday, December 12, 2017 1. First, you need to create
The Number Devil: A Mathematical Adventure -By Hans Magnus Enzensberger 2 nd 9 wks Honors Math Journal Project Mrs. C. Thompson's Math Class DUE: Tuesday, December 12, 2017 1. First, you need to create
Proceedings of the Third International DERIVE/TI-92 Conference
 Description of the TI-92 Plus Module Doing Advanced Mathematics with the TI-92 Plus Module Carl Leinbach Gettysburg College Bert Waits Ohio State University leinbach@cs.gettysburg.edu waitsb@math.ohio-state.edu
Description of the TI-92 Plus Module Doing Advanced Mathematics with the TI-92 Plus Module Carl Leinbach Gettysburg College Bert Waits Ohio State University leinbach@cs.gettysburg.edu waitsb@math.ohio-state.edu
Journey through Mathematics
 Journey through Mathematics Enrique A. González-Velasco Journey through Mathematics Creative Episodes in Its History Enrique A. González-Velasco Department of Mathematical Sciences University of Massachusetts
Journey through Mathematics Enrique A. González-Velasco Journey through Mathematics Creative Episodes in Its History Enrique A. González-Velasco Department of Mathematical Sciences University of Massachusetts
CAP Student Feedback Survey
 CAP Student Feedback Survey Name of teacher: Date: Directions: Read each statement and then choose one answer choice that you think fits best. There are no right or wrong answers. Your teacher will use
CAP Student Feedback Survey Name of teacher: Date: Directions: Read each statement and then choose one answer choice that you think fits best. There are no right or wrong answers. Your teacher will use
Study Guide. Solutions to Selected Exercises. Foundations of Music and Musicianship with CD-ROM. 2nd Edition. David Damschroder
 Study Guide Solutions to Selected Exercises Foundations of Music and Musicianship with CD-ROM 2nd Edition by David Damschroder Solutions to Selected Exercises 1 CHAPTER 1 P1-4 Do exercises a-c. Remember
Study Guide Solutions to Selected Exercises Foundations of Music and Musicianship with CD-ROM 2nd Edition by David Damschroder Solutions to Selected Exercises 1 CHAPTER 1 P1-4 Do exercises a-c. Remember
REPORT ON THE NOVEMBER 2009 EXAMINATIONS
 THEORY OF MUSIC REPORT ON THE NOVEMBER 2009 EXAMINATIONS General Accuracy and neatness are crucial at all levels. In the earlier grades there were examples of notes covering more than one pitch, whilst
THEORY OF MUSIC REPORT ON THE NOVEMBER 2009 EXAMINATIONS General Accuracy and neatness are crucial at all levels. In the earlier grades there were examples of notes covering more than one pitch, whilst
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWare http://ocw.mit.edu 18.06 Linear Algebra, Spring 2005 Please use the following citation format: Gilbert Strang, 18.06 Linear Algebra, Spring 2005. (Massachusetts Institute of Technology:
MIT OpenCourseWare http://ocw.mit.edu 18.06 Linear Algebra, Spring 2005 Please use the following citation format: Gilbert Strang, 18.06 Linear Algebra, Spring 2005. (Massachusetts Institute of Technology:
Math: Fractions and Decimals 105
 Math: Fractions and Decimals 105 Many students face fractions with trepidation; they re too hard, I don t understand. If this is you, there is no better tool to bring yourself back up to speed than a tape
Math: Fractions and Decimals 105 Many students face fractions with trepidation; they re too hard, I don t understand. If this is you, there is no better tool to bring yourself back up to speed than a tape
Overview. Teacher s Manual and reproductions of student worksheets to support the following lesson objective:
 Overview Lesson Plan #1 Title: Ace it! Lesson Nine Attached Supporting Documents for Plan #1: Teacher s Manual and reproductions of student worksheets to support the following lesson objective: Find products
Overview Lesson Plan #1 Title: Ace it! Lesson Nine Attached Supporting Documents for Plan #1: Teacher s Manual and reproductions of student worksheets to support the following lesson objective: Find products
E314: Conjecture sur la raison de quelques dissonances generalement recues dans la musique
 Translation of Euler s paper with Notes E314: Conjecture sur la raison de quelques dissonances generalement recues dans la musique (Conjecture on the Reason for some Dissonances Generally Heard in Music)
Translation of Euler s paper with Notes E314: Conjecture sur la raison de quelques dissonances generalement recues dans la musique (Conjecture on the Reason for some Dissonances Generally Heard in Music)
North Carolina Standard Course of Study - Mathematics
 A Correlation of To the North Carolina Standard Course of Study - Mathematics Grade 4 A Correlation of, Grade 4 Units Unit 1 - Arrays, Factors, and Multiplicative Comparison Unit 2 - Generating and Representing
A Correlation of To the North Carolina Standard Course of Study - Mathematics Grade 4 A Correlation of, Grade 4 Units Unit 1 - Arrays, Factors, and Multiplicative Comparison Unit 2 - Generating and Representing
Lesson 25: Solving Problems in Two Ways Rates and Algebra
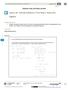 : Solving Problems in Two Ways Rates and Algebra Student Outcomes Students investigate a problem that can be solved by reasoning quantitatively and by creating equations in one variable. They compare the
: Solving Problems in Two Ways Rates and Algebra Student Outcomes Students investigate a problem that can be solved by reasoning quantitatively and by creating equations in one variable. They compare the
Mobile Math Teachers Circle The Return of the iclicker
 Mobile Math Teachers Circle The Return of the iclicker June 20, 2016 1. Dr. Spock asked his class to solve a percent problem, Julia set up the proportion: 4/5 = x/100. She then cross-multiplied to solve
Mobile Math Teachers Circle The Return of the iclicker June 20, 2016 1. Dr. Spock asked his class to solve a percent problem, Julia set up the proportion: 4/5 = x/100. She then cross-multiplied to solve
Display Dilemma. Display Dilemma. 1 of 12. Copyright 2008, Exemplars, Inc. All rights reserved.
 I visited friends in New York City during the summer. They took me to this HUGE Wal-Mart store. There was a display of cookie boxes that I could not believe! The display was in a pyramid shape with at
I visited friends in New York City during the summer. They took me to this HUGE Wal-Mart store. There was a display of cookie boxes that I could not believe! The display was in a pyramid shape with at
Immanuel Kant Critique of Pure Reason
 Immanuel Kant Critique of Pure Reason THE A PRIORI GROUNDS OF THE POSSIBILITY OF EXPERIENCE THAT a concept, although itself neither contained in the concept of possible experience nor consisting of elements
Immanuel Kant Critique of Pure Reason THE A PRIORI GROUNDS OF THE POSSIBILITY OF EXPERIENCE THAT a concept, although itself neither contained in the concept of possible experience nor consisting of elements
Non-decimal Slide Adders 1 and the Carry
 Stephan Weiss Non-decimal Slide Adders 1 and the Carry I'm sure everyone knows those small thin adders with parallel arranged and hookshaped slots. They were mainly used for additions and subtractions.
Stephan Weiss Non-decimal Slide Adders 1 and the Carry I'm sure everyone knows those small thin adders with parallel arranged and hookshaped slots. They were mainly used for additions and subtractions.
Trimester 2 5 th Grade Name: Answer Key
 Trimester 2 th Grade Name: Answer Key..NBT.7 Fiona hiked along a trail in Glacier National Park that is 7.2 miles long. It took her hours to hike. What was her average speed per hour? 7.2 / =.3 (miles
Trimester 2 th Grade Name: Answer Key..NBT.7 Fiona hiked along a trail in Glacier National Park that is 7.2 miles long. It took her hours to hike. What was her average speed per hour? 7.2 / =.3 (miles
Key Curriculum Press th Street, Emeryville, CA
 Resource Overview Skill or Concept: Model or compute with integers using addition or subtraction. (QT N 261) Excerpted from: Key Curriculum Press 1150 65th Street, Emeryville, CA 94608 www.keypress.com
Resource Overview Skill or Concept: Model or compute with integers using addition or subtraction. (QT N 261) Excerpted from: Key Curriculum Press 1150 65th Street, Emeryville, CA 94608 www.keypress.com
The Nature of Time. Humberto R. Maturana. November 27, 1995.
 The Nature of Time Humberto R. Maturana November 27, 1995. I do not wish to deal with all the domains in which the word time enters as if it were referring to an obvious aspect of the world or worlds that
The Nature of Time Humberto R. Maturana November 27, 1995. I do not wish to deal with all the domains in which the word time enters as if it were referring to an obvious aspect of the world or worlds that
Fixed-Point Calculator
 Fixed-Point Calculator Robert Kozubiak, Muris Zecevic, Cameron Renny Electrical and Computer Engineering Department School of Engineering and Computer Science Oakland University, Rochester, MI rjkozubiak@oakland.edu,
Fixed-Point Calculator Robert Kozubiak, Muris Zecevic, Cameron Renny Electrical and Computer Engineering Department School of Engineering and Computer Science Oakland University, Rochester, MI rjkozubiak@oakland.edu,
MIT Alumni Books Podcast The Proof and the Pudding
 MIT Alumni Books Podcast The Proof and the Pudding JOE This is the MIT Alumni Books Podcast. I'm Joe McGonegal, Director of Alumni Education. My guest, Jim Henle, Ph.D. '76, is the Myra M. Sampson Professor
MIT Alumni Books Podcast The Proof and the Pudding JOE This is the MIT Alumni Books Podcast. I'm Joe McGonegal, Director of Alumni Education. My guest, Jim Henle, Ph.D. '76, is the Myra M. Sampson Professor
How Mathematics and Art Are Interconnected. Liz Sweetwood. October 24th, 2016
 How Mathematics and Art Are Interconnected Liz Sweetwood October 24th, 2016 2 Throughout time, Art has been an outlet for a creator to openly express themselves and the way they see the world around them.
How Mathematics and Art Are Interconnected Liz Sweetwood October 24th, 2016 2 Throughout time, Art has been an outlet for a creator to openly express themselves and the way they see the world around them.
Uses of Fractions. Fractions
 Uses of The numbers,,,, and are all fractions. A fraction is written with two whole numbers that are separated by a fraction bar. The top number is called the numerator. The bottom number is called the
Uses of The numbers,,,, and are all fractions. A fraction is written with two whole numbers that are separated by a fraction bar. The top number is called the numerator. The bottom number is called the
Formula of the sieve of Eratosthenes. Abstract
 Formula of the sieve of Eratosthenes Prof. and Ing. Jose de Jesus Camacho Medina Pepe9mx@yahoo.com.mx Http://matematicofresnillense.blogspot.mx Fresnillo, Zacatecas, Mexico. Abstract This article offers
Formula of the sieve of Eratosthenes Prof. and Ing. Jose de Jesus Camacho Medina Pepe9mx@yahoo.com.mx Http://matematicofresnillense.blogspot.mx Fresnillo, Zacatecas, Mexico. Abstract This article offers
A Child Thinking About Infinity
 A Child Thinking About Infinity David Tall Mathematics Education Research Centre University of Warwick COVENTRY CV4 7AL Young children s thinking about infinity can be fascinating stories of extrapolation
A Child Thinking About Infinity David Tall Mathematics Education Research Centre University of Warwick COVENTRY CV4 7AL Young children s thinking about infinity can be fascinating stories of extrapolation
Scientific Philosophy
 Scientific Philosophy Gustavo E. Romero IAR-CONICET/UNLP, Argentina FCAGLP, UNLP, 2018 Philosophy of mathematics The philosophy of mathematics is the branch of philosophy that studies the philosophical
Scientific Philosophy Gustavo E. Romero IAR-CONICET/UNLP, Argentina FCAGLP, UNLP, 2018 Philosophy of mathematics The philosophy of mathematics is the branch of philosophy that studies the philosophical
History of Math for the Liberal Arts CHAPTER 4. The Pythagoreans. Lawrence Morales. Seattle Central Community College
 1 3 4 History of Math for the Liberal Arts 5 6 CHAPTER 4 7 8 The Pythagoreans 9 10 11 Lawrence Morales 1 13 14 Seattle Central Community College MAT107 Chapter 4, Lawrence Morales, 001; Page 1 15 16 17
1 3 4 History of Math for the Liberal Arts 5 6 CHAPTER 4 7 8 The Pythagoreans 9 10 11 Lawrence Morales 1 13 14 Seattle Central Community College MAT107 Chapter 4, Lawrence Morales, 001; Page 1 15 16 17
Lecture 3: Nondeterministic Computation
 IAS/PCMI Summer Session 2000 Clay Mathematics Undergraduate Program Basic Course on Computational Complexity Lecture 3: Nondeterministic Computation David Mix Barrington and Alexis Maciel July 19, 2000
IAS/PCMI Summer Session 2000 Clay Mathematics Undergraduate Program Basic Course on Computational Complexity Lecture 3: Nondeterministic Computation David Mix Barrington and Alexis Maciel July 19, 2000
Sequential Storyboards introduces the storyboard as visual narrative that captures key ideas as a sequence of frames unfolding over time
 Section 4 Snapshots in Time: The Visual Narrative What makes interaction design unique is that it imagines a person s behavior as they interact with a system over time. Storyboards capture this element
Section 4 Snapshots in Time: The Visual Narrative What makes interaction design unique is that it imagines a person s behavior as they interact with a system over time. Storyboards capture this element
INTERVALS Ted Greene
 1 INTERVALS The interval is to music as the atom is to matter the basic essence of the stuff. All music as we know it is composed of intervals, which in turn make up scales or melodies, which in turn make
1 INTERVALS The interval is to music as the atom is to matter the basic essence of the stuff. All music as we know it is composed of intervals, which in turn make up scales or melodies, which in turn make
A ROMANTICIZED RETROSPECTION TO THE PAST?! A Synopsis on Cornerpoints of LOGO - discussion published in german-written journals
 A ROMANTICIZED RETROSPECTION TO THE PAST?! A Synopsis on Cornerpoints of LOGO - discussion published in german-written journals Daniela Bräml Karl Fuchs Abstract Papert promotes LOGO as a very effective
A ROMANTICIZED RETROSPECTION TO THE PAST?! A Synopsis on Cornerpoints of LOGO - discussion published in german-written journals Daniela Bräml Karl Fuchs Abstract Papert promotes LOGO as a very effective
1.1 The Language of Mathematics Expressions versus Sentences
 . The Language of Mathematics Expressions versus Sentences a hypothetical situation the importance of language Study Strategies for Students of Mathematics characteristics of the language of mathematics
. The Language of Mathematics Expressions versus Sentences a hypothetical situation the importance of language Study Strategies for Students of Mathematics characteristics of the language of mathematics
EXPONENTS EXPLORATION 12. Does folding a piece of paper in half multiple times explain everything there is to know about the powers of two?
 EXPLORATION EXPONENTS Does folding a piece of paper in half multiple times explain everything there is to know about the powers of two? TOPICS COVERED: Exponents and their properties. James Tanton 9 A.
EXPLORATION EXPONENTS Does folding a piece of paper in half multiple times explain everything there is to know about the powers of two? TOPICS COVERED: Exponents and their properties. James Tanton 9 A.
BC Sequences and series 2015.notebook March 03, 2015
 Feb 25 12:49 PM 1 Jan 27 9:13 AM 2 Jan 27 9:24 AM 3 Feb 25 12:49 PM 4 Warm up thoughts What notation is used for sequences? What notation is used for series? How are they related? Jan 13 8:01 AM 5 Limit
Feb 25 12:49 PM 1 Jan 27 9:13 AM 2 Jan 27 9:24 AM 3 Feb 25 12:49 PM 4 Warm up thoughts What notation is used for sequences? What notation is used for series? How are they related? Jan 13 8:01 AM 5 Limit
A Process of the Fusion of Horizons in the Text Interpretation
 A Process of the Fusion of Horizons in the Text Interpretation Kazuya SASAKI Rikkyo University There is a philosophy, which takes a circle between the whole and the partial meaning as the necessary condition
A Process of the Fusion of Horizons in the Text Interpretation Kazuya SASAKI Rikkyo University There is a philosophy, which takes a circle between the whole and the partial meaning as the necessary condition
MITOCW big_picture_integrals_512kb-mp4
 MITOCW big_picture_integrals_512kb-mp4 PROFESSOR: Hi. Well, if you're ready, this will be the other big side of calculus. We still have two functions, as before. Let me call them the height and the slope:
MITOCW big_picture_integrals_512kb-mp4 PROFESSOR: Hi. Well, if you're ready, this will be the other big side of calculus. We still have two functions, as before. Let me call them the height and the slope:
Roman Road Primary School
 Roman Road Primary School Presentation Policy Written September 2016 Reviewed September 2017 Next review September 2020 Tehira Aslam 1 Roman Road Presentation Policy Aims To establish high expectations
Roman Road Primary School Presentation Policy Written September 2016 Reviewed September 2017 Next review September 2020 Tehira Aslam 1 Roman Road Presentation Policy Aims To establish high expectations
Source/Receiver (SR) Setup
 PS User Guide Series 2015 Source/Receiver (SR) Setup For 1-D and 2-D Vs Profiling Prepared By Choon B. Park, Ph.D. January 2015 Table of Contents Page 1. Overview 2 2. Source/Receiver (SR) Setup Main Menu
PS User Guide Series 2015 Source/Receiver (SR) Setup For 1-D and 2-D Vs Profiling Prepared By Choon B. Park, Ph.D. January 2015 Table of Contents Page 1. Overview 2 2. Source/Receiver (SR) Setup Main Menu
Mathematics in India: From Vedic Period To Modern Times Prof. K. Ramasubramanian Indian Institute of Technology-Bombay
 Mathematics in India: From Vedic Period To Modern Times Prof. K. Ramasubramanian Indian Institute of Technology-Bombay Lecture-6 Decimal place value system When this lecture will be discussing the decimal
Mathematics in India: From Vedic Period To Modern Times Prof. K. Ramasubramanian Indian Institute of Technology-Bombay Lecture-6 Decimal place value system When this lecture will be discussing the decimal
Sample file. Copyright Taina Maria Miller. EDITION 1.2
 Copyright 2008-2011 Taina Maria Miller. EDITION 1.2 All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, or by any information
Copyright 2008-2011 Taina Maria Miller. EDITION 1.2 All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, or by any information
The transition from understanding the operation of a simple adder, built during a sixth-form science session, to understanding how a full sized
 The transition from understanding the operation of a simple adder, built during a sixth-form science session, to understanding how a full sized digital computer can through-put vast amounts of scientific
The transition from understanding the operation of a simple adder, built during a sixth-form science session, to understanding how a full sized digital computer can through-put vast amounts of scientific
Background to Gottlob Frege
 Background to Gottlob Frege Gottlob Frege (1848 1925) Life s work: logicism (the reduction of arithmetic to logic). This entailed: Inventing (discovering?) modern logic, including quantification, variables,
Background to Gottlob Frege Gottlob Frege (1848 1925) Life s work: logicism (the reduction of arithmetic to logic). This entailed: Inventing (discovering?) modern logic, including quantification, variables,
THE INDIAN KEYBOARD. Gjalt Wijmenga
 THE INDIAN KEYBOARD Gjalt Wijmenga 2015 Contents Foreword 1 Introduction A Scales - The notion pure or epimoric scale - 3-, 5- en 7-limit scales 3 B Theory planimetric configurations of interval complexes
THE INDIAN KEYBOARD Gjalt Wijmenga 2015 Contents Foreword 1 Introduction A Scales - The notion pure or epimoric scale - 3-, 5- en 7-limit scales 3 B Theory planimetric configurations of interval complexes
Linking Words / Phrases
 Linking Words / Phrases Personal opinion: To list advantages and disadvantages: In my opinion/ In my view / To my mind / To my way of thinking / I am convinced that / It strikes me that / It is my firm
Linking Words / Phrases Personal opinion: To list advantages and disadvantages: In my opinion/ In my view / To my mind / To my way of thinking / I am convinced that / It strikes me that / It is my firm
The Public Libraries in East Berlin
 The Public Libraries in East Berlin HEINZ WERNER IN ORDER TO BETTER UN ERSTAN the presentday trends in the development of the public library system in Berlin (capital city of the German Democratic Republic),
The Public Libraries in East Berlin HEINZ WERNER IN ORDER TO BETTER UN ERSTAN the presentday trends in the development of the public library system in Berlin (capital city of the German Democratic Republic),
Mathematical Principles of Fuzzy Logic
 Mathematical Principles of Fuzzy Logic THE KLUWER INTERNATIONAL SERIES IN ENGINEERING AND COMPUTER SCIENCE MATHEMATICAL PRINCIPLES OF FUZZY LOGIC VILEM N O V K University of Ostrava Institute for Research
Mathematical Principles of Fuzzy Logic THE KLUWER INTERNATIONAL SERIES IN ENGINEERING AND COMPUTER SCIENCE MATHEMATICAL PRINCIPLES OF FUZZY LOGIC VILEM N O V K University of Ostrava Institute for Research
Encoders and Decoders: Details and Design Issues
 Encoders and Decoders: Details and Design Issues Edward L. Bosworth, Ph.D. TSYS School of Computer Science Columbus State University Columbus, GA 31907 bosworth_edward@colstate.edu Slide 1 of 25 slides
Encoders and Decoders: Details and Design Issues Edward L. Bosworth, Ph.D. TSYS School of Computer Science Columbus State University Columbus, GA 31907 bosworth_edward@colstate.edu Slide 1 of 25 slides
Section A Using the n th Term Formula Grade D / C
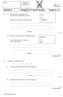 Name: Teacher Assessment Section A Using the n th Term Formula Grade D / C 1. The first term of a sequence is 2. The rule for continuing the sequence is What is the second term of the sequence? Add 7 then
Name: Teacher Assessment Section A Using the n th Term Formula Grade D / C 1. The first term of a sequence is 2. The rule for continuing the sequence is What is the second term of the sequence? Add 7 then
Design Document Ira Bray
 Description of the Instructional Problem In most public libraries volunteers play an important role in supporting staff. The volunteer services can be varied, some involve Friends of the Library book sales
Description of the Instructional Problem In most public libraries volunteers play an important role in supporting staff. The volunteer services can be varied, some involve Friends of the Library book sales
AskDrCallahan Calculus 1 Teacher s Guide
 AskDrCallahan Calculus 1 Teacher s Guide 3rd Edition rev 080108 Dale Callahan, Ph.D., P.E. Lea Callahan, MSEE, P.E. Copyright 2008, AskDrCallahan, LLC v3-r080108 www.askdrcallahan.com 2 Welcome to AskDrCallahan
AskDrCallahan Calculus 1 Teacher s Guide 3rd Edition rev 080108 Dale Callahan, Ph.D., P.E. Lea Callahan, MSEE, P.E. Copyright 2008, AskDrCallahan, LLC v3-r080108 www.askdrcallahan.com 2 Welcome to AskDrCallahan
in the Howard County Public School System and Rocketship Education
 Technical Appendix May 2016 DREAMBOX LEARNING ACHIEVEMENT GROWTH in the Howard County Public School System and Rocketship Education Abstract In this technical appendix, we present analyses of the relationship
Technical Appendix May 2016 DREAMBOX LEARNING ACHIEVEMENT GROWTH in the Howard County Public School System and Rocketship Education Abstract In this technical appendix, we present analyses of the relationship
Length of thesis In correspondence with instructions on the internet by other institutions, the following recommendations are given:
 Humboldt-Universität zu Berlin Faculty of Life Sciences Thaer-Institute Berlin, August 2014 Guidance on the submission of final theses at the Faculty of Life Sciences, Thaer-Institute 0.The purpose of
Humboldt-Universität zu Berlin Faculty of Life Sciences Thaer-Institute Berlin, August 2014 Guidance on the submission of final theses at the Faculty of Life Sciences, Thaer-Institute 0.The purpose of
1/10. The A-Deduction
 1/10 The A-Deduction Kant s transcendental deduction of the pure concepts of understanding exists in two different versions and this week we are going to be looking at the first edition version. After
1/10 The A-Deduction Kant s transcendental deduction of the pure concepts of understanding exists in two different versions and this week we are going to be looking at the first edition version. After
AREA OF KNOWLEDGE: MATHEMATICS
 AREA OF KNOWLEDGE: MATHEMATICS Introduction Mathematics: the rational mind is at work. When most abstracted from the world, mathematics stands apart from other areas of knowledge, concerned only with its
AREA OF KNOWLEDGE: MATHEMATICS Introduction Mathematics: the rational mind is at work. When most abstracted from the world, mathematics stands apart from other areas of knowledge, concerned only with its
K12 Course Introductions. Introduction to Music K12 Inc. All rights reserved
 K12 Course Introductions Introduction to Music 2000-04 K12 Inc. All rights reserved Music About the Singing Voice How to Teach Your Child to Sing What to Do With the Reluctant Singer Terms and Concepts
K12 Course Introductions Introduction to Music 2000-04 K12 Inc. All rights reserved Music About the Singing Voice How to Teach Your Child to Sing What to Do With the Reluctant Singer Terms and Concepts
Formal Concept Analysis
 Formal Concept Analysis Springer Berlin Heidelberg New York Barcelona Hong Kong London Milan Paris Singapore Tokyo Bernhard Ganter Rudolf Wille Formal Concept Analysis Mathematical Foundations With 105
Formal Concept Analysis Springer Berlin Heidelberg New York Barcelona Hong Kong London Milan Paris Singapore Tokyo Bernhard Ganter Rudolf Wille Formal Concept Analysis Mathematical Foundations With 105
SPEED DRILL WARM-UP ACTIVITY
 SPEED DRILL WARM-UP ACTIVITY Name the operation representative of each of the following: percent left reduction total more half less twice off lower each double Write the equivalents: 20% as a decimal
SPEED DRILL WARM-UP ACTIVITY Name the operation representative of each of the following: percent left reduction total more half less twice off lower each double Write the equivalents: 20% as a decimal
Piano Performance Grade SYLLABUS. Valid from Current until further notice. Issued by authority of the
 Yamaha Grade Examination System Piano Performance Grade Grade 6 SYLLABUS Valid from 2014 Current until further notice Issued by authority of the Copyright 2013 by YAMAHA MUSIC FOUNDATION All Rights Reserved.
Yamaha Grade Examination System Piano Performance Grade Grade 6 SYLLABUS Valid from 2014 Current until further notice Issued by authority of the Copyright 2013 by YAMAHA MUSIC FOUNDATION All Rights Reserved.
What Does Sticker Notation Mean For Math
 What Does Sticker Mean For Math Free PDF ebook Download: What Does Sticker Mean For Math Download or Read Online ebook what does sticker notation mean for math in PDF Format From The Best User Guide Database
What Does Sticker Mean For Math Free PDF ebook Download: What Does Sticker Mean For Math Download or Read Online ebook what does sticker notation mean for math in PDF Format From The Best User Guide Database
The Calculative Calculator
 The Calculative Calculator Interactive Digital Calculator Chandler Connolly, Sarah Elhage, Matthew Shina, Daniyah Alaswad Electrical and Computer Engineering Department School of Engineering and Computer
The Calculative Calculator Interactive Digital Calculator Chandler Connolly, Sarah Elhage, Matthew Shina, Daniyah Alaswad Electrical and Computer Engineering Department School of Engineering and Computer
My Book Of Money: Dollars And Cents PDF
 My Book Of Money: Dollars And Cents PDF This sequel to My First Book of Money helps children make the difficult transition between cents and dollars. By first reviewing the names and values of coins, and
My Book Of Money: Dollars And Cents PDF This sequel to My First Book of Money helps children make the difficult transition between cents and dollars. By first reviewing the names and values of coins, and
(Skip to step 11 if you are already familiar with connecting to the Tribot)
 LEGO MINDSTORMS NXT Lab 5 Remember back in Lab 2 when the Tribot was commanded to drive in a specific pattern that had the shape of a bow tie? Specific commands were passed to the motors to command how
LEGO MINDSTORMS NXT Lab 5 Remember back in Lab 2 when the Tribot was commanded to drive in a specific pattern that had the shape of a bow tie? Specific commands were passed to the motors to command how
1/6. The Anticipations of Perception
 1/6 The Anticipations of Perception The Anticipations of Perception treats the schematization of the category of quality and is the second of Kant s mathematical principles. As with the Axioms of Intuition,
1/6 The Anticipations of Perception The Anticipations of Perception treats the schematization of the category of quality and is the second of Kant s mathematical principles. As with the Axioms of Intuition,
Date: Autumn Topic: Playlist RE BIG QUESTION:
 Music Science Geography Art and Design PSHE PE Computing Music Week 1: Engage L1: Engage- LO Can I give a personal response to a performance? show the children a performance by Hogwarts Symphony Orchestra.
Music Science Geography Art and Design PSHE PE Computing Music Week 1: Engage L1: Engage- LO Can I give a personal response to a performance? show the children a performance by Hogwarts Symphony Orchestra.
MARK SCHEME for the November 2004 question paper 9702 PHYSICS
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Advanced Level MARK SCHEME for the November 2004 question paper 9702 PHYSICS 9702/05 Paper 5 (Practical Test), maximum raw mark 30 This mark scheme
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS GCE Advanced Level MARK SCHEME for the November 2004 question paper 9702 PHYSICS 9702/05 Paper 5 (Practical Test), maximum raw mark 30 This mark scheme
The Lazy Man Explains the Irrational. E. L. Lady
 The Lazy Man Explains the Irrational E. L. Lady I ve been thinking about those numbers that you can t write as fractions, Mr. Tinker said. Irrational numbers, they re called, the Lazy Man answered. Well,
The Lazy Man Explains the Irrational E. L. Lady I ve been thinking about those numbers that you can t write as fractions, Mr. Tinker said. Irrational numbers, they re called, the Lazy Man answered. Well,
Transducers and Sensors
 Transducers and Sensors Dr. Ibrahim Al-Naimi Chapter THREE Transducers and Sensors 1 Digital transducers are defined as transducers with a digital output. Transducers available at large are primary analogue
Transducers and Sensors Dr. Ibrahim Al-Naimi Chapter THREE Transducers and Sensors 1 Digital transducers are defined as transducers with a digital output. Transducers available at large are primary analogue
Fig. I.1 The Fields Medal.
 INTRODUCTION The world described by the natural and the physical sciences is a concrete and perceptible one: in the first approximation through the senses, and in the second approximation through their
INTRODUCTION The world described by the natural and the physical sciences is a concrete and perceptible one: in the first approximation through the senses, and in the second approximation through their
IF MONTY HALL FALLS OR CRAWLS
 UDK 51-05 Rosenthal, J. IF MONTY HALL FALLS OR CRAWLS CHRISTOPHER A. PYNES Western Illinois University ABSTRACT The Monty Hall problem is consistently misunderstood. Mathematician Jeffrey Rosenthal argues
UDK 51-05 Rosenthal, J. IF MONTY HALL FALLS OR CRAWLS CHRISTOPHER A. PYNES Western Illinois University ABSTRACT The Monty Hall problem is consistently misunderstood. Mathematician Jeffrey Rosenthal argues
Monadology and Music 2: Leibniz s Demon
 Monadology and Music 2: Leibniz s Demon Soshichi Uchii (Kyoto University, Emeritus) Abstract Drawing on my previous paper Monadology and Music (Uchii 2015), I will further pursue the analogy between Monadology
Monadology and Music 2: Leibniz s Demon Soshichi Uchii (Kyoto University, Emeritus) Abstract Drawing on my previous paper Monadology and Music (Uchii 2015), I will further pursue the analogy between Monadology
Example the number 21 has the following pairs of squares and numbers that produce this sum.
 by Philip G Jackson info@simplicityinstinct.com P O Box 10240, Dominion Road, Mt Eden 1446, Auckland, New Zealand Abstract Four simple attributes of Prime Numbers are shown, including one that although
by Philip G Jackson info@simplicityinstinct.com P O Box 10240, Dominion Road, Mt Eden 1446, Auckland, New Zealand Abstract Four simple attributes of Prime Numbers are shown, including one that although
Table of Contents. Introduction...v. About the CD-ROM...vi. Standards Correlations... vii. Ratios and Proportional Relationships...
 Table of Contents Introduction...v About the CD-ROM...vi Standards Correlations... vii Ratios and Proportional Relationships... 1 The Number System... 10 Expressions and Equations... 23 Geometry... 27
Table of Contents Introduction...v About the CD-ROM...vi Standards Correlations... vii Ratios and Proportional Relationships... 1 The Number System... 10 Expressions and Equations... 23 Geometry... 27
2 nd Int. Conf. CiiT, Molika, Dec CHAITIN ARTICLES
 2 nd Int. Conf. CiiT, Molika, 20-23.Dec.2001 93 CHAITIN ARTICLES D. Gligoroski, A. Dimovski Institute of Informatics, Faculty of Natural Sciences and Mathematics, Sts. Cyril and Methodius University, Arhimedova
2 nd Int. Conf. CiiT, Molika, 20-23.Dec.2001 93 CHAITIN ARTICLES D. Gligoroski, A. Dimovski Institute of Informatics, Faculty of Natural Sciences and Mathematics, Sts. Cyril and Methodius University, Arhimedova
EC6302-DIGITAL ELECTRONICS II YEAR /III SEMESTER ECE ACADEMIC YEAR
 LECTURER NOTES ON EC6302-DIGITAL ELECTRONICS II YEAR /III SEMESTER ECE ACADEMIC YEAR 2014-2015 D.ANTONYPANDIARAJAN ASSISTANT PROFESSOR FMCET Introduction: The English mathematician George Boole (1815-1864)
LECTURER NOTES ON EC6302-DIGITAL ELECTRONICS II YEAR /III SEMESTER ECE ACADEMIC YEAR 2014-2015 D.ANTONYPANDIARAJAN ASSISTANT PROFESSOR FMCET Introduction: The English mathematician George Boole (1815-1864)
Sets, Symbols and Pictures: A Reflection on Euler Diagrams in Leonhard Euler s Tercentenary (2007)
 Mediterranean Journal for Research in Mathematics Education Vol. 5, 2, 77-82, 2006 Sets, Symbols and Pictures: A Reflection on Euler Diagrams in Leonhard Euler s Tercentenary (2007) GIORGIO T. BAGNI: Department
Mediterranean Journal for Research in Mathematics Education Vol. 5, 2, 77-82, 2006 Sets, Symbols and Pictures: A Reflection on Euler Diagrams in Leonhard Euler s Tercentenary (2007) GIORGIO T. BAGNI: Department
MODULE 3. Combinational & Sequential logic
 MODULE 3 Combinational & Sequential logic Combinational Logic Introduction Logic circuit may be classified into two categories. Combinational logic circuits 2. Sequential logic circuits A combinational
MODULE 3 Combinational & Sequential logic Combinational Logic Introduction Logic circuit may be classified into two categories. Combinational logic circuits 2. Sequential logic circuits A combinational
NUMB3RS Activity: Coded Messages. Episode: The Mole
 Teacher Page 1 : Coded Messages Topic: Inverse Matrices Grade Level: 10-11 Objective: Students will learn how to apply inverse matrix multiplication to the coding of values. Time: 15 minutes Materials:
Teacher Page 1 : Coded Messages Topic: Inverse Matrices Grade Level: 10-11 Objective: Students will learn how to apply inverse matrix multiplication to the coding of values. Time: 15 minutes Materials:
SPIRE MATHS Stimulating, Practical, Interesting, Relevant, Enjoyable Maths For All
 Ratio and proportion TYPE: Main OBJECTIVE(S): Understand the relationship between ratio and proportion; use ratio notation, reduce a ratio to its simplest form and divide a quantity into two parts in a
Ratio and proportion TYPE: Main OBJECTIVE(S): Understand the relationship between ratio and proportion; use ratio notation, reduce a ratio to its simplest form and divide a quantity into two parts in a
Fallacies and Paradoxes
 Fallacies and Paradoxes The sun and the nearest star, Alpha Centauri, are separated by empty space. Empty space is nothing. Therefore nothing separates the sun from Alpha Centauri. If nothing
Fallacies and Paradoxes The sun and the nearest star, Alpha Centauri, are separated by empty space. Empty space is nothing. Therefore nothing separates the sun from Alpha Centauri. If nothing
Bar Codes to the Rescue!
 Fighting Computer Illiteracy or How Can We Teach Machines to Read Spring 2013 ITS102.23 - C 1 Bar Codes to the Rescue! If it is hard to teach computers how to read ordinary alphabets, create a writing
Fighting Computer Illiteracy or How Can We Teach Machines to Read Spring 2013 ITS102.23 - C 1 Bar Codes to the Rescue! If it is hard to teach computers how to read ordinary alphabets, create a writing
Out of Italy. New in the Renaissance (Springboard handout) Living Legend (2 page handout) What s the Difference? (handout)
 Out of Italy Springboard: Students should study the New in the Renaissance chronology and answer the questions. (Printing and books along with trade and traveling artists and scholars helped spread the
Out of Italy Springboard: Students should study the New in the Renaissance chronology and answer the questions. (Printing and books along with trade and traveling artists and scholars helped spread the
Route optimization using Hungarian method combined with Dijkstra's in home health care services
 Research Journal of Computer and Information Technology Sciences ISSN 2320 6527 Route optimization using Hungarian method combined with Dijkstra's method in home health care services Abstract Monika Sharma
Research Journal of Computer and Information Technology Sciences ISSN 2320 6527 Route optimization using Hungarian method combined with Dijkstra's method in home health care services Abstract Monika Sharma
INTRODUCTION TO AXIOMATIC SET THEORY
 INTRODUCTION TO AXIOMATIC SET THEORY SYNTHESE LIBRARY MONOGRAPHS ON EPISTEMOLOGY, LOGIC, METHODOLOGY, PHILOSOPHY OF SCIENCE, SOCIOLOGY OF SCIENCE AND OF KNOWLEDGE, AND ON THE MATHEMATICAL METHODS OF SOCIAL
INTRODUCTION TO AXIOMATIC SET THEORY SYNTHESE LIBRARY MONOGRAPHS ON EPISTEMOLOGY, LOGIC, METHODOLOGY, PHILOSOPHY OF SCIENCE, SOCIOLOGY OF SCIENCE AND OF KNOWLEDGE, AND ON THE MATHEMATICAL METHODS OF SOCIAL
Many findings in archaeology bear witness to some math in
 Beginnings The Early Days Many findings in archaeology bear witness to some math in the mind of our ancestors. There are many scholarly books on that matter, but we may be content with a few examples.
Beginnings The Early Days Many findings in archaeology bear witness to some math in the mind of our ancestors. There are many scholarly books on that matter, but we may be content with a few examples.
THESIS MIND AND WORLD IN KANT S THEORY OF SENSATION. Submitted by. Jessica Murski. Department of Philosophy
 THESIS MIND AND WORLD IN KANT S THEORY OF SENSATION Submitted by Jessica Murski Department of Philosophy In partial fulfillment of the requirements For the Degree of Master of Arts Colorado State University
THESIS MIND AND WORLD IN KANT S THEORY OF SENSATION Submitted by Jessica Murski Department of Philosophy In partial fulfillment of the requirements For the Degree of Master of Arts Colorado State University
The XYZ Colour Space. 26 January 2011 WHITE PAPER. IMAGE PROCESSING TECHNIQUES
 www.omnitek.tv IMAE POESSIN TEHNIQUES The olour Space The colour space has the unique property of being able to express every colour that the human eye can see which in turn means that it can express every
www.omnitek.tv IMAE POESSIN TEHNIQUES The olour Space The colour space has the unique property of being able to express every colour that the human eye can see which in turn means that it can express every
GCSE MARKING SCHEME AUTUMN 2017 GCSE MATHEMATICS NUMERACY UNIT 1 - INTERMEDIATE TIER 3310U30-1. WJEC CBAC Ltd.
 GCSE MARKING SCHEME AUTUMN 2017 GCSE MATHEMATICS NUMERACY UNIT 1 - INTERMEDIATE TIER 3310U30-1 INTRODUCTION This marking scheme was used by WJEC for the 2017 examination. It was finalised after detailed
GCSE MARKING SCHEME AUTUMN 2017 GCSE MATHEMATICS NUMERACY UNIT 1 - INTERMEDIATE TIER 3310U30-1 INTRODUCTION This marking scheme was used by WJEC for the 2017 examination. It was finalised after detailed
