Note: Please use the actual date you accessed this material in your citation.
|
|
|
- Patrick Smith
- 5 years ago
- Views:
Transcription
1 MIT OpenCourseWare Linear Algebra, Spring 2005 Please use the following citation format: Gilbert Strang, Linear Algebra, Spring (Massachusetts Institute of Technology: MIT OpenCourseWare). (accessed MM DD, YYYY). License: Creative Commons Attribution- Noncommercial-Share Alike. Note: Please use the actual date you accessed this material in your citation. For more information about citing these materials or our Terms of Use, visit:
2 MIT OpenCourseWare Linear Algebra, Spring 2005 Transcript Lecture 3 I've been multiplying matrices already, but certainly time for me to discuss the rules for matrix multiplication. And the interesting part is the many ways you can do it, and they all give the same answer. And they're all important. So matrix multiplication, and then, come inverses. So we mentioned the inverse of a matrix. That's a big deal. Lots to do about inverses and how to find them. Okay, so I'll begin with how to multiply two matrices. First way, okay, so suppose I have a matrix A multiplying a matrix B and -- giving me a result -- well, I could call it C. A times B. Okay. So, let me just review the rule for this entry. That's the entry in row i and column j. So that's the i j entry. Right there is C i j. We always write the row number and then the column number. So I might -- I might -- maybe I take it C 3 4, just to make it specific. So instead of i j, let me use numbers. C 3 4. So where does that come from, the three four entry? It comes from row three, here, row three and column four, as you know. Column four. And can I just write down, or can we write down the formula for it? If we look at the whole row and the whole column, the quick way for me to say it is row three of A -- I could use a dot for dot product. I won't often use that, actually. Dot column four of B. But this gives us a chance to just, like, use a little matrix notation. What are the entries? What's this first entry in row three? That number that's sitting right there is... A, so it's got two indices and what are they? 3 1. So there's an a 3 1 there. Now what's the first guy at the top of column four? So what's sitting up there? B 1 4, right. So that this dot product starts with A 3 1 times B 1 4. And then what's the next -- so this is like I'm accumulating this sum, then comes the next guy, A 3 2, second column, times B 2 4, second row. So it's b A 3 2, B 2 4 and so on.
3 Just practice with indices. Oh, let me even practice with a summation formula. So this is -- most of the course, I use whole vectors. I very seldom, get down to the details of these particular entries, but here we'd better do it. So it's some kind of a sum, right? Of things in row three, column K shall I say? Times things in row K, column four. Do you see that that's what we're seeing here? This is K is one, here K is two, on along -- so the sum goes all the way along the row and down the column, say, one to N. So that's what the C three four entry looks like. A sum of a three K b K four. Just takes a little practice to do that. Okay. And -- well, maybe I should say -- when are we allowed to multiply these matrices? What are the shapes of these things? The shapes are -- if we allow them to be not necessarily square matrices. If they're square, they've got to be the same size. If they're rectangular, they're not the same size. If they're rectangular, this might be -- well, I always think of A as m by n. m rows, n columns. So that sum goes to n. Now what's the point -- how many rows does B have to have? n. The number of rows in B, the number of guys that we meet coming down has to match the number of ones across. So B will have to be n by something. Whatever. P. So the number of columns here has to match the number of rows there, and then what's the result? What's the shape of the result? What's the shape of C, the output? Well, it's got these same m rows -- it's got m rows. And how many columns? P. m by P. Okay. So there are m times P little numbers in there, entries, and each one, looks like that. Okay. So that's the standard rule. That's the way people think of multiplying matrices. I do it too. But I want to talk about other ways to look at that same calculation, looking at whole columns and whole rows. Okay. So can I do A B C again? A B equaling C again? But now, tell me about... I'll put it up here. So here goes A, again, times B producing C. And again, this is m by n. This is n by P and this is m by P. Okay. Now I want to look at whole columns. I want to look at the columns of -- here's the second way to multiply matrices. Because I'm going to build on what I know already. How do I multiply a matrix by a column? I know how to multiply this matrix by that column. Shall I call that column one? That tells me column one of the answer.
4 The matrix times the first column is that first column. Because none of this stuff entered that part of the answer. The matrix times the second column is the second column of the answer. Do you see what I'm saying? That I could think of multiplying a matrix by a vector, which I already knew how to do, and I can think of just P columns sitting side by side, just like resting next to each other. And I multiply A times each one of those. And I get the P columns of the answer. Do you see this as -- this is quite nice, to be able to think, okay, matrix multiplication works so that I can just think of having several columns, multiplying by A and getting the columns of the answer. So, like, here's column one shall I call that column one? And what's going in there is A times column one. Okay. So that's the picture a column at a time. So what does that tell me? What does that tell me about these columns? These columns of C are combinations, because we've seen that before, of columns of A. Every one of these comes from A times this, and A times a vector is a combination of the columns of A. And it makes sense, because the columns of A have length m and the columns of C have length m. And every column of C is some combination of the columns of A. And it's these numbers in here that tell me what combination it is. Do you see that? That in that answer, C, I'm seeing stuff that's combinations of these columns. Now, suppose I look at it -- that's two ways now. The third way is look at it by rows. So now let me change to rows. Okay. So now I can think of a row of A -- a row of A multiplying all these rows here and producing a row of the product. So this row takes a combination of these rows and that's the answer. So these rows of C are combinations of what? Tell me how to finish that. The rows of C, when I have a matrix B, it's got its rows and I multiply by A, and what does that do? It mixes the rows up. It creates combinations of the rows of B, thanks. Rows of B. That's what I wanted to see, that this answer -- I can see where the pieces are coming from. The rows in the answer are coming as combinations of these rows. The columns in the answer are coming as combinations of those columns. And so that's three ways. Now you can say, okay, what's the fourth way? The fourth way -- so that's -- now we've got, like, the regular way, the column way, the row way and -- what's left? The one that I can -- well, one way is columns times rows. What happens if I multiply -- So this was row times column, it gave a number. Okay.
5 Now I want to ask you about column times row. If I multiply a column of A times a row of B, what shape I ending up with? So if I take a column times a row, that's definitely different from taking a row times a column. So a column of A was -- what's the shape of a column of A? n by one. A column of A is a column. It's got m entries and one column. And what's a row of B? It's got one row and P columns. So what's the shape -- what do I get if I multiply a column by a row? I get a big matrix. I get a full-sized matrix. If I multiply a column by a row -- should we just do one? Let me take the column two three four times the row one six. That product there -- I mean, when I'm just following the rules of matrix multiplication, those rules are just looking like -- kind of petite, kind of small, because the rows here are so short and the columns there are so short, but they're the same length, one entry. So what's the answer? What's the answer if I do two three four times one six, just for practice? Well, what's the first row of the answer? Two twelve. And the second row of the answer is three eighteen. And the third row of the answer is four twenty four. That's a very special matrix, there. Very special matrix. What can you tell me about its columns, the columns of that matrix? They're multiples of this guy, right? They're multiples of that one. Which follows our rule. We said that the columns of the answer were combinations, but there's only -- to take a combination of one guy, it's just a multiple. The rows of the answer, what can you tell me about those three rows? They're all multiples of this row. They're all multiples of one six, as we expected. But I'm getting a full-sized matrix. And now, just to complete this thought, if I have -- let me write down the fourth way. A B is a sum of columns of A times rows of B. So that, for example, if my matrix was two three four and then had another column, say, seven eight nine, and my matrix here has -- say, started with one six and then had another column like zero zero, then -- here's the fourth way, okay? I've got two columns there, I've got two rows there. So the beautiful rule is -- see, the whole thing by columns and rows is that I can take the first column times the first row and add the second column times the second row. So that's the fourth way -- that I can take columns times rows, first column times first row, second column times second row and add. Actually, what will I get? What will the answer be for that matrix multiplication? Well, this one it's just going to give us zero, so in fact I'm back to this -- that's the answer, for that matrix multiplication. I'm happy to put up here these facts about matrix multiplication, because it gives me a chance to write down special matrices like this. This is a special matrix. All those rows lie on the same line. All those rows lie on the line through one six. If I draw a picture of all these row vectors, they're all the same direction.
6 If I draw a picture of these two column vectors, they're in the same direction. Later, I would use this language. Not too much later, either. I would say the row space, which is like all the combinations of the rows, is just a line for this matrix. The row space is the line through the vector one six. All the rows lie on that line. And the column space is also a line. All the columns lie on the line through the vector two three four. So this is like a really minimal matrix. And it's because of these ones. Okay. So that's a third way. Now I want to say one more thing about matrix multiplication while we're on the subject. And it's this. You could also multiply -- You could also cut the matrix into blocks and do the multiplication by blocks. Yet that's actually so, useful that I want to mention it. Block multiplication. So I could take my matrix A and I could chop it up, like, maybe just for simplicity, let me chop it into two -- into four square blocks. Suppose it's square. Let's just take a nice case. And B, suppose it's square also, same size. So these sizes don't have to be the same. What they have to do is match properly. Here they certainly will match. So here's the rule for block multiplication, that if this has blocks like, A -- so maybe A1, A2, A3, A4 are the blocks here, and these blocks are B1, B2,3 and B4? Then the answer I can find block. And if you tell me what's in that block, then I'm going to be quiet about matrix multiplication for the rest of the day. What goes into that block? You see, these might be -- this matrix might be -- these matrices might be, like, twenty by twenty with blocks that are ten by ten, to take the easy case where all the blocks are the same shape. And the point is that I could multiply those by blocks. And what goes in here? What's that block in the answer? A1 B1, that's a matrix times a matrix, it's the right size, ten by ten. Any more? Plus, what else goes in there? A2 B3, right? It's just like block rows times block columns. Nobody, I think, not even Gauss could see instantly that it works. But somehow, if we check it through, all five ways we're doing the same multiplications. So this familiar multiplication is what we're really doing when we do it by columns, by rows by columns times rows and by blocks. Okay. I just have to, like, get the rules straight for matrix multiplication. Okay. All right, I'm ready for the second topic, which is inverses. Okay. Ready for inverses. And let me do it for square matrices first. Okay. So I've got a square matrix A. And it may or may not have an inverse, right? Not all matrices have inverses. In fact, that's the most important question you can ask
7 about the matrix, is if it's -- if you know it's square, is it invertible or not? If it is invertible, then there is some other matrix, shall I call it A inverse? And what's the -- if A inverse exists -- there's a big "if" here. If this matrix exists, and it'll be really central to figure out when does it exist? And then if it does exist, how would you find it? But what's the equation here that I haven't -- that I have to finish now? This matrix, if it exists multiplies A and produces, I think, the identity. But a real -- an inverse for a square matrix could be on the right as well -- this is true, too, that it's -- if I have a -- yeah in fact, this is not -- this is probably the -- this is something that's not easy to prove, but it works. That a left -- square matrices, a left inverse is also a right inverse. If I can find a matrix on the left that gets the identity, then also that matrix on the right will produce that identity. For rectangular matrices, we'll see a left inverse that isn't a right inverse. In fact, the shapes wouldn't allow it. But for square matrices, the shapes allow it and it happens, if A has an inverse. Okay, so give me some cases -- let's see. I hate to be negative here, but let's talk about the case with no inverse. So -- these matrices are called invertible or non-singular -- those are the good ones. And we want to be able to identify how -- if we're given a matrix, has it got an inverse? Can I talk about the singular case? No inverse. All right. Best to start with an example. Tell me an example -- let's get an example up here. Let's make it two by two -- of a matrix that has not got an inverse. And let's see why. Let me write one up. No inverse. Let's see why. Let me write up -- one three two six. Why does that matrix have no inverse? You could answer that various ways. Give me one reason. Well, you could -- if you know about determinants, which you're not supposed to, you could take its determinant and you would get -- Zero. Okay. Now -- all right. Let me ask you other reasons. I mean, as for other reasons that that matrix isn't invertible. Here, I could use what I'm saying here. Suppose A times other matrix gave the identity. Why is that not possible? Because -- oh, yeah -- I'm thinking about columns here. If I multiply this matrix A by some other matrix, then the -- the result -- what can you tell me about the columns? They're all multiples of those columns, right? If I multiply A by another matrix that -- the product has columns that come from those columns. So can I get the identity matrix? No way. The columns of the identity matrix, like one zero -- it's not a combination of those columns, because those two columns lie on the -- both lie on the same line. Every combination is just going to be on that line and I can't get one zero.
8 So, do you see that sort of column picture of the matrix not being invertible. In fact, here's another reason. This is even a more important reason. Well, how can I say more important? All those are important. This is another way to see it. A matrix has no inverse -- yeah -- here -- now this is important. A matrix has no -- a square matrix won't have an inverse if there's no inverse because I can solve -- I can find an X of -- a vector X with A times -- this A times X giving zero. This is the reason I like best. That matrix won't have an inverse. Can you -- well, let me change I to U. So tell me a vector X that, solves A X equals zero. I mean, this is, like, the key equation. In mathematics, all the key equations have zero on the right-hand side. So what's the X? Tell me an X here -- so now I'm going to put -- slip in the X that you tell me and I'm going to get zero. What X would do that job? Three and negative one? Is that the one you picked, or -- yeah. Or another -- well, if you picked zero with zero, I'm not so excited, right? Because that would always work. So it's really the fact that this vector isn't zero that's important. It's a non-zero vector and three negative one would do it. That just says three of this column minus one of that column is the zero column. Okay. So now I know that A couldn't be invertible. But what's the reasoning? If A X is zero, suppose I multiplied by A inverse. Yeah, well here's the reason. Here -- this is why this spells disaster for an inverse. The matrix can't have an inverse if some combination of the columns gives z- it gives nothing. Because, I could take A X equals zero, I could multiply by A inverse and what would I discover? Suppose I take that equation and I multiply by -- if A inverse existed, which of course I'm going to come to the conclusion it can't because if it existed, if there was an A inverse to this dopey matrix, I would multiply that equation by that inverse and I would discover X is zero. If I multiply A by A inverse on the left, I get X. If I multiply by A inverse on the right, I get zero. So I would discover X was zero. But it -- X is not zero.
9 X -- this guy wasn't zero. There it is. It's three minus one. So, conclusion -- only, it takes us some time to really work with that conclusion -- our conclusion will be that non-invertible matrices, singular matrices, some combinations of their columns gives the zero column. They they take some vector X into zero. And there's no way A inverse can recover, right? That's what this equation says. This equation says I take this vector X and multiplying by A gives zero. But then when I multiply by A inverse, I can never escape from zero. So there couldn't be an A inverse. Where here -- okay, now fix -- all right. Now let me take -- all right, back to the positive side. Let's take a matrix that does have an inverse. And why not invert it? Okay. Can I -- so let me take on this third board a matrix -- shall I fix that up a little? Tell me a matrix that has got an inverse. Well, let me say one three two -- what shall I put there? Well, don't put six, I guess is -- right? Do I any favorites here? One? Or eight? I don't care. What, seven? Seven. Okay. Seven is a lucky number. All right, seven, okay. Okay. So -- now what's our idea? We believe that this matrix is invertible. Those who like determinants have quickly taken its determinant and found it wasn't zero. Those who like columns, and probably that -- that department is not totally popular yet -- but those who like columns will look at those two columns and say, hey, they point in different directions. So I can get anything. Now, let me see, what do I mean? How I going to computer A inverse? So A inverse -- here's A inverse, now, and I have to find it. And what do I get when I do this multiplication? The identity. You know, forgive me for taking two by two-s, but -- lt's good to keep the computations manageable and let the ideas come out. Okay, now what's the idea I want? I'm looking for this matrix A inverse, how I going to find it? Right now, I've got four numbers to find. I'm going to look at the first column. Let me take this first column, A B. What's up there? What -- tell me this. What equation does the first column satisfy? The first column satisfies A times that column is one zero. The first column of the answer. And the second column, C D, satisfies A times that second column is zero one. You see that finding the inverse is like solving two systems. One system, when the right-hand side is one zero -- I'm just going to split it into two pieces. I don't even need to rewrite it. I can take A times -- so let me put
10 it here. A times column j of A inverse is column j of the identity. I've got n equations. I've got, well, two in this case. And they have the same matrix, A, but they have different right-hand sides. The right-hand sides are just the columns of the identity, this guy and this guy. And these are the two solutions. Do you see what I'm going -- I'm looking at that equation by columns. I'm looking at A times this column, giving that guy, and A times that column giving that guy. So -- Essentially -- so this is like the Gauss -- we're back to Gauss. We're back to solving systems of equations, but we're solving -- we've got two righthand sides instead of one. That's where Jordan comes in. So at the very beginning of the lecture, I mentioned Gauss-Jordan, let me write it up again. Okay. Here's the Gauss-Jordan idea. Gauss-Jordan solve two equations at once. Okay. Let me show you how the mechanics go. How do I solve a single equation? So the two equations are one three two seven, multiplying A B gives one zero. And the other equation is the same one three two seven multiplying C D gives zero one. Okay. That'll tell me the two columns of the inverse. I'll have inverse. In other words, if I can solve with this matrix A, if I can solve with that right-hand side and that right-hand side, I'm invertible. I've got it. Okay. And Jordan sort of said to Gauss, solve them together, look at the matrix -- if we just solve this one, I would look at one three two seven, and how do I deal with the right-hand side? I stick it on as an extra column, right? That's this augmented matrix. That's the matrix when I'm watching the right-hand side at the same time, doing the same thing to the right side that I do to the left? So I just carry it along as an extra column. Now I'm going to carry along two extra columns. And I'm going to do whatever Gauss wants, right? I'm going to do elimination. I'm going to get this to be simple and this thing will turn into the inverse. This is what's coming. I'm going to do elimination steps to make this into the identity, and lo and behold, the inverse will show up here. K--- let's do it. Okay. So what are the elimination steps? So you see -- here's my matrix A and here's the identity, like, stuck on, augmented on. STUDENT: I'm sorry... STRANG: Yeah? STUDENT: -- is the two and the three supposed to be switched? STRANG: Did I -- oh, no, they weren't supposed to be switched. Sorry. Thanks. Okay.
11 Thank you very much. And there -- I've got them right. Okay, thanks. Okay. So let's do elimination. All right, it's going to be simple, right? So I take two of this row away from this row. So this row stays the same and two of those come away from this. That leaves me with a zero and a one and two of these away from this is that what you're getting -- after one elimination step -- Let me sort of separate the -- the left half from the right half. So two of that first row got subtracted from the second row. Now this is an upper triangular form. Gauss would quit, but Jordan says keeps going. Use elimination upwards. Subtract a multiple of equation two from equation one to get rid of the three. So let's go the whole way. So now I'm going to -- this guy is fine, but I'm going to -- what do I do now? What's my final step that produces the inverse? I multiply this by the right number to get up to ther to remove that three. So I guess, I -- since this is a one, there's the pivot sitting there. I multiply it by three and subtract from that, so what do I get? I'll have one zero -- oh, yeah that was my whole point. I'll multiply this by three and subtract from that, which will give me seven. And I multiply this by three and subtract from that, which gives me a minus three. And what's my hope, belief? Here I started with A and the identity, and I ended up with the identity and who? That better be A inverse. That's the Gauss Jordan idea. Start with this long matrix, double-length A I, eliminate, eliminate until this part is down to I, then this one will -- must be for some reason, and we've got to find the reason -- must be A inverse. Shall I just check that it works? Let me just check that -- can I multiply this matrix this part times A, I'll carry A over here and just do that multiplication. You'll see I'll do it the old fashioned way. Seven minus six is a one. Twenty one minus twenty one is a zero, minus two plus two is a zero, minus six plus seven is a one. Check. So that is the inverse. That's the Gauss-Jordan idea. So, you'll -- one of the homework problems or more than one for Wednesday will ask you to go through those steps. I think you just got to go through Gauss-Jordan a couple of times, but I -- yeah -- just to see the mechanics. But the, important thing is, why -- is, like, what happened? Why did we -- why did we get A inverse there? Let me ask you that. We got -- so we take -- We do row reduction, we do elimination on this long matrix A I until the first half is up. Then a second half is A inverse.
12 Well, how do I see that? Let me put up here how I see that. So here's my Gauss- Jordan thing, and I'm doing stuff to it. So I'm -- well, whole lot of E's. Remember those are those elimination matrices. Those are the -- those are the things that we figured out last time. Yes, that's what an elimination step is it's in matrix form, I'm multiplying by some Es. And the result -- well, so I'm multiplying by a whole bunch of Es. So, I get a -- can I call the overall matrix E? That's the elimination matrix, the product of all those little pieces. What do I mean by little pieces? Well, there was an elimination matrix that subtracted two of that away from that. Then there was an elimination matrix that subtracted three of that away from that. I guess in this case, that was all. So there were just two Es in this case, one that did this step and one that did this step and together they gave me an E that does both steps. And the net result was to get an I here. And you can tell me what that has to be. This is, like, the picture of what happened. If E multiplied A, whatever that E is -- we never figured it out in this way. But whatever that E times that E is, E times A is -- What's E times A? It's I. That E, whatever the heck it was, multiplied A and produced I. So E must be -- E A equaling I tells us what E is, namely it is -- STUDENT: It's the inverse of A. STRANG: It's the inverse of A. Great. And therefore, when the second half, when E multiplies I, it's E -- Put this A inverse. You see the picture looking that way? E times A is the identity. It tells us what E has to be. It has to be the inverse, and therefore, on the right-hand side, where E -- where we just smartly tucked on the identity, it's turning in, step by step -- It's turning into A inverse. There is the statement of Gauss-Jordan elimination. That's how you find the inverse. Where we can look at it as elimination, as solving n equations at the same time and tacking on n columns, solving those equations and up goes the n columns of A inverse. Okay, thanks. See you on Wednesday.
MITOCW ocw f08-lec19_300k
 MITOCW ocw-18-085-f08-lec19_300k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
MITOCW ocw-18-085-f08-lec19_300k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
MITOCW big_picture_integrals_512kb-mp4
 MITOCW big_picture_integrals_512kb-mp4 PROFESSOR: Hi. Well, if you're ready, this will be the other big side of calculus. We still have two functions, as before. Let me call them the height and the slope:
MITOCW big_picture_integrals_512kb-mp4 PROFESSOR: Hi. Well, if you're ready, this will be the other big side of calculus. We still have two functions, as before. Let me call them the height and the slope:
MITOCW max_min_second_der_512kb-mp4
 MITOCW max_min_second_der_512kb-mp4 PROFESSOR: Hi. Well, I hope you're ready for second derivatives. We don't go higher than that in many problems, but the second derivative is an important-- the derivative
MITOCW max_min_second_der_512kb-mp4 PROFESSOR: Hi. Well, I hope you're ready for second derivatives. We don't go higher than that in many problems, but the second derivative is an important-- the derivative
DIFFERENTIATE SOMETHING AT THE VERY BEGINNING THE COURSE I'LL ADD YOU QUESTIONS USING THEM. BUT PARTICULAR QUESTIONS AS YOU'LL SEE
 1 MATH 16A LECTURE. OCTOBER 28, 2008. PROFESSOR: SO LET ME START WITH SOMETHING I'M SURE YOU ALL WANT TO HEAR ABOUT WHICH IS THE MIDTERM. THE NEXT MIDTERM. IT'S COMING UP, NOT THIS WEEK BUT THE NEXT WEEK.
1 MATH 16A LECTURE. OCTOBER 28, 2008. PROFESSOR: SO LET ME START WITH SOMETHING I'M SURE YOU ALL WANT TO HEAR ABOUT WHICH IS THE MIDTERM. THE NEXT MIDTERM. IT'S COMING UP, NOT THIS WEEK BUT THE NEXT WEEK.
Transcript: Reasoning about Exponent Patterns: Growing, Growing, Growing
 Transcript: Reasoning about Exponent Patterns: Growing, Growing, Growing 5.1-2 1 This transcript is the property of the Connected Mathematics Project, Michigan State University. This publication is intended
Transcript: Reasoning about Exponent Patterns: Growing, Growing, Growing 5.1-2 1 This transcript is the property of the Connected Mathematics Project, Michigan State University. This publication is intended
MITOCW ocw f07-lec02_300k
 MITOCW ocw-18-01-f07-lec02_300k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
MITOCW ocw-18-01-f07-lec02_300k The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free.
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWare http://ocw.mit.edu 18.03 Differential Equations, Spring 2006 Please use the following citation format: Arthur Mattuck and Haynes Miller, 18.03 Differential Equations, Spring 2006. (Massachusetts
MIT OpenCourseWare http://ocw.mit.edu 18.03 Differential Equations, Spring 2006 Please use the following citation format: Arthur Mattuck and Haynes Miller, 18.03 Differential Equations, Spring 2006. (Massachusetts
MITOCW Lec 3 MIT 6.042J Mathematics for Computer Science, Fall 2010
 MITOCW Lec 3 MIT 6.042J Mathematics for Computer Science, Fall 2010 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality
MITOCW Lec 3 MIT 6.042J Mathematics for Computer Science, Fall 2010 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality
Description: PUP Math Brandon interview Location: Conover Road School Colts Neck, NJ Researcher: Professor Carolyn Maher
 Page: 1 of 8 Line Time Speaker Transcript 1. Narrator When the researchers gave them the pizzas with four toppings problem, most of the students made lists of toppings and counted their combinations. But
Page: 1 of 8 Line Time Speaker Transcript 1. Narrator When the researchers gave them the pizzas with four toppings problem, most of the students made lists of toppings and counted their combinations. But
PROFESSOR: I'd like to welcome you to this course on computer science. Actually, that's a terrible way to start.
 MITOCW Lecture 1A [MUSIC PLAYING] PROFESSOR: I'd like to welcome you to this course on computer science. Actually, that's a terrible way to start. Computer science is a terrible name for this business.
MITOCW Lecture 1A [MUSIC PLAYING] PROFESSOR: I'd like to welcome you to this course on computer science. Actually, that's a terrible way to start. Computer science is a terrible name for this business.
MIT Alumni Books Podcast The Proof and the Pudding
 MIT Alumni Books Podcast The Proof and the Pudding JOE This is the MIT Alumni Books Podcast. I'm Joe McGonegal, Director of Alumni Education. My guest, Jim Henle, Ph.D. '76, is the Myra M. Sampson Professor
MIT Alumni Books Podcast The Proof and the Pudding JOE This is the MIT Alumni Books Podcast. I'm Joe McGonegal, Director of Alumni Education. My guest, Jim Henle, Ph.D. '76, is the Myra M. Sampson Professor
MITOCW MIT7_01SCF11_track01_300k.mp4
 MITOCW MIT7_01SCF11_track01_300k.mp4 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for
MITOCW MIT7_01SCF11_track01_300k.mp4 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for
PROFESSOR: Well, last time we talked about compound data, and there were two main points to that business.
 MITOCW Lecture 3A [MUSIC PLAYING] PROFESSOR: Well, last time we talked about compound data, and there were two main points to that business. First of all, there was a methodology of data abstraction, and
MITOCW Lecture 3A [MUSIC PLAYING] PROFESSOR: Well, last time we talked about compound data, and there were two main points to that business. First of all, there was a methodology of data abstraction, and
So just by way of a little warm up exercise, I'd like you to look at that integration problem over there. The one
 MITOCW Lec-02 What we're going to talk about today, is goals. So just by way of a little warm up exercise, I'd like you to look at that integration problem over there. The one that's disappeared. So the
MITOCW Lec-02 What we're going to talk about today, is goals. So just by way of a little warm up exercise, I'd like you to look at that integration problem over there. The one that's disappeared. So the
Night of the Cure. TUCKER, late 20s. ELI, mid-40s. CHRIS, mid-30s
 Night of the Cure TUCKER, late 20s. ELI, mid-40s. CHRIS, mid-30s Setting: A heavy door. Above, a flickering neon sign that reads "Touche" or "Sidetrack." Something not nearly clever enough. Time: Six months
Night of the Cure TUCKER, late 20s. ELI, mid-40s. CHRIS, mid-30s Setting: A heavy door. Above, a flickering neon sign that reads "Touche" or "Sidetrack." Something not nearly clever enough. Time: Six months
The following content is provided under a Creative Commons license. Your support
 MITOCW Lecture 17 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a
MITOCW Lecture 17 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a
Contractions Contraction
 Contraction 1. Positive : I'm I am I'm waiting for my friend. I've I have I've worked here for many years. I'll I will/i shall I'll see you tomorrow. I'd I would/i should/i had I'd better leave now. I'd
Contraction 1. Positive : I'm I am I'm waiting for my friend. I've I have I've worked here for many years. I'll I will/i shall I'll see you tomorrow. I'd I would/i should/i had I'd better leave now. I'd
Dominque Silva: I'm Dominique Silva, I am a senior here at Chico State, as well as a tutor in the SLC, I tutor math up to trig, I've been here, this
 Dominque Silva: I'm Dominique Silva, I am a senior here at Chico State, as well as a tutor in the SLC, I tutor math up to trig, I've been here, this now my fourth semester, I'm graduating finally in May.
Dominque Silva: I'm Dominique Silva, I am a senior here at Chico State, as well as a tutor in the SLC, I tutor math up to trig, I've been here, this now my fourth semester, I'm graduating finally in May.
MITOCW watch?v=vifkgfl1cn8
 MITOCW watch?v=vifkgfl1cn8 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
MITOCW watch?v=vifkgfl1cn8 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
Um... yes, I know that. (laugh) You don't need to introduce yourself!
 Machigai Podcast Episode 023 Hello, this is Machigai English School. Hello, Tim? My name is Yukino! Um... yes, I know that. (laugh) You don't need to introduce yourself! Well, I want to make sure you know
Machigai Podcast Episode 023 Hello, this is Machigai English School. Hello, Tim? My name is Yukino! Um... yes, I know that. (laugh) You don't need to introduce yourself! Well, I want to make sure you know
Our Dad is in Atlantis
 Our Dad is in Atlantis by Javier Malpica Translated by Jorge Ignacio Cortiñas 4 October 2006 Characters Big Brother : an eleven year old boy Little Brother : an eight year old boy Place Mexico Time The
Our Dad is in Atlantis by Javier Malpica Translated by Jorge Ignacio Cortiñas 4 October 2006 Characters Big Brother : an eleven year old boy Little Brother : an eight year old boy Place Mexico Time The
how two ex-students turned on to pure mathematics and found total happiness a mathematical novelette by D. E. Knuth SURREAL NUMBERS -A ADDISON WESLEY
 how two ex-students turned on to pure mathematics and found total happiness a mathematical novelette by D. E. Knuth SURREAL NUMBERS -A ADDISON WESLEY 1 THE ROCK /..,..... A. Bill, do you think you've found
how two ex-students turned on to pure mathematics and found total happiness a mathematical novelette by D. E. Knuth SURREAL NUMBERS -A ADDISON WESLEY 1 THE ROCK /..,..... A. Bill, do you think you've found
I HAD TO STAY IN BED. PRINT PAGE 161. Chapter 11
 PRINT PAGE 161. Chapter 11 I HAD TO STAY IN BED a whole week after that. That bugged me; I'm not the kind that can lie around looking at the ceiling all the time. I read most of the time, and drew pictures.
PRINT PAGE 161. Chapter 11 I HAD TO STAY IN BED a whole week after that. That bugged me; I'm not the kind that can lie around looking at the ceiling all the time. I read most of the time, and drew pictures.
Richard Hoadley Thanks Kevin. Now, I'd like each of you to use your keyboards to try and reconstruct some of the complexities of those sounds.
 The sound of silence Recreating sounds Alan's told me that instruments sound different, because of the mixture of harmonics that go with the fundamental. I've got a recording of his saxophone here, a sound
The sound of silence Recreating sounds Alan's told me that instruments sound different, because of the mixture of harmonics that go with the fundamental. I've got a recording of his saxophone here, a sound
MITOCW mit-6-00-f08-lec17_300k
 MITOCW mit-6-00-f08-lec17_300k OPERATOR: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources
MITOCW mit-6-00-f08-lec17_300k OPERATOR: The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources
_The_Power_of_Exponentials,_Big and Small_
 _The_Power_of_Exponentials,_Big and Small_ Nataly, I just hate doing this homework. I know. Exponentials are a huge drag. Yeah, well, now that you mentioned it, let me tell you a story my grandmother once
_The_Power_of_Exponentials,_Big and Small_ Nataly, I just hate doing this homework. I know. Exponentials are a huge drag. Yeah, well, now that you mentioned it, let me tell you a story my grandmother once
Life without Library Systems?
 Life without Library Systems? Written by Debby Emerson Adapted and illustrated By Christine McGinty and Elly Dawson 20 Published by Pioneer Library System 2005 Once upon a time there was a girl named Katie
Life without Library Systems? Written by Debby Emerson Adapted and illustrated By Christine McGinty and Elly Dawson 20 Published by Pioneer Library System 2005 Once upon a time there was a girl named Katie
The Focus = C Major Scale/Progression/Formula: C D E F G A B - ( C )
 Chord Progressions 101 The Major Progression Formula The Focus = C Major Scale/Progression/Formula: C D E F G A B - ( C ) The first things we need to understand are: 1. Chords come from the scale with
Chord Progressions 101 The Major Progression Formula The Focus = C Major Scale/Progression/Formula: C D E F G A B - ( C ) The first things we need to understand are: 1. Chords come from the scale with
Display Contest Submittals
 Display Contest Submittals #1a ----- Original Message ----- From: Jim Horn To: rjnelsoncf@cox.net Sent: Tuesday, April 28, 2009 3:07 PM Subject: Interesting calculator display Hi, Richard Well, it takes
Display Contest Submittals #1a ----- Original Message ----- From: Jim Horn To: rjnelsoncf@cox.net Sent: Tuesday, April 28, 2009 3:07 PM Subject: Interesting calculator display Hi, Richard Well, it takes
ECO LECTURE TWENTY-THREE 1 OKAY. WE'RE GETTING TO GO ON AND TALK ABOUT THE LONG-RUN
 ECO 155 750 LECTURE TWENTY-THREE 1 OKAY. WE'RE GETTING TO GO ON AND TALK ABOUT THE LONG-RUN EQUILIBRIUM FOR THE ECONOMY. BUT BEFORE WE DO, I WANT TO FINISH UP ON SOMETHING I WAS TALKING ABOUT LAST TIME.
ECO 155 750 LECTURE TWENTY-THREE 1 OKAY. WE'RE GETTING TO GO ON AND TALK ABOUT THE LONG-RUN EQUILIBRIUM FOR THE ECONOMY. BUT BEFORE WE DO, I WANT TO FINISH UP ON SOMETHING I WAS TALKING ABOUT LAST TIME.
Look Mom, I Got a Job!
 Look Mom, I Got a Job! by T. James Belich T. James Belich tjamesbelich@gmail.com www.tjamesbelich.com Look Mom, I Got a Job! by T. James Belich CHARACTERS (M), an aspiring actor with a less-than-inspiring
Look Mom, I Got a Job! by T. James Belich T. James Belich tjamesbelich@gmail.com www.tjamesbelich.com Look Mom, I Got a Job! by T. James Belich CHARACTERS (M), an aspiring actor with a less-than-inspiring
LLT 180 Lecture 8 1. We're over on page 194. We had just gotten done. We had Wart saying clearly
 LLT 180 Lecture 8 1 We're over on page 194. We had just gotten done. We had Wart saying clearly what we all knew and we beat it up that he much preferred the geese to the ant. And now finally we get rid
LLT 180 Lecture 8 1 We're over on page 194. We had just gotten done. We had Wart saying clearly what we all knew and we beat it up that he much preferred the geese to the ant. And now finally we get rid
The following content is provided under a Creative Commons license. Your support
 MITOCW Lecture 6 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation
MITOCW Lecture 6 The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation
DOCUMENT NAME/INFORMANT: PETER CHAMBERLAIN #2 INFORMANT'S ADDRESS: INTERVIEW LOCATION: TRIBE/NATION: OOWEKEENO HISTORY PROJECT
 DOCUMENT NAME/INFORMANT: PETER CHAMBERLAIN #2 INFORMANT'S ADDRESS: INTERVIEW LOCATION: TRIBE/NATION: LANGUAGE: ENGLISH DATE OF INTERVIEW: 09/3-9/76 INTERVIEWER: DAVID STEVENSON INTERPRETER: TRANSCRIBER:
DOCUMENT NAME/INFORMANT: PETER CHAMBERLAIN #2 INFORMANT'S ADDRESS: INTERVIEW LOCATION: TRIBE/NATION: LANGUAGE: ENGLISH DATE OF INTERVIEW: 09/3-9/76 INTERVIEWER: DAVID STEVENSON INTERPRETER: TRANSCRIBER:
Our Story Of How It All Began
 Our Story Of How It All Began This story begins on March 13, 2013 when Mark texted Kristin, "Hey, this is Mark. Glad we met tonight" Our Story Of How It All Began 1 Then Kristin replied, "Hi! Me too :)"
Our Story Of How It All Began This story begins on March 13, 2013 when Mark texted Kristin, "Hey, this is Mark. Glad we met tonight" Our Story Of How It All Began 1 Then Kristin replied, "Hi! Me too :)"
Our Story Of How It All Began
 Our Story Of How It All Began This story begins on March 13, 2013 when Mark texted Kristin, "Hey, this is Mark. Glad we met tonight" 1 Kristin went on, "Hi! Me too :)" Mark said, "Here's that photo of
Our Story Of How It All Began This story begins on March 13, 2013 when Mark texted Kristin, "Hey, this is Mark. Glad we met tonight" 1 Kristin went on, "Hi! Me too :)" Mark said, "Here's that photo of
Video - low carb for doctors (part 8)
 Video - low carb for doctors (part 8) Dr. David Unwin: I'm fascinated really by the idea that so many of the modern diseases we have now are about choices that we all make, lifestyle choices. And if we
Video - low carb for doctors (part 8) Dr. David Unwin: I'm fascinated really by the idea that so many of the modern diseases we have now are about choices that we all make, lifestyle choices. And if we
On the eve of the Neil Young and Crazy Horse Australian tour, he spoke with Undercover's Paul Cashmere.
 Undercover Greendale (interview with poncho) Sometime in the 90's Neil Young was christened the Godfather of Grunge but the title really belonged to his band Crazy Horse. While Young has jumped through
Undercover Greendale (interview with poncho) Sometime in the 90's Neil Young was christened the Godfather of Grunge but the title really belonged to his band Crazy Horse. While Young has jumped through
Bite Size Brownies. Designed by: Jonathan Thompson George Mason University, COMPLETE Math
 Bite Size Brownies Designed by: Jonathan Thompson George Mason University, COMPLETE Math The Task Mr. Brown E. Pan recently opened a new business making brownies called The Brown E. Pan. On his first day
Bite Size Brownies Designed by: Jonathan Thompson George Mason University, COMPLETE Math The Task Mr. Brown E. Pan recently opened a new business making brownies called The Brown E. Pan. On his first day
Installing a Turntable and Operating it Under AI Control
 Installing a Turntable and Operating it Under AI Control Turntables can be found on many railroads, from the smallest to the largest, and their ability to turn locomotives in a relatively small space makes
Installing a Turntable and Operating it Under AI Control Turntables can be found on many railroads, from the smallest to the largest, and their ability to turn locomotives in a relatively small space makes
THE BENCH PRODUCTION HISTORY
 THE BENCH CONTACT INFORMATION Paula Fell (310) 497-6684 paulafell@cox.net 3520 Fifth Avenue Corona del Mar, CA 92625 BIOGRAPHY My experience in the theatre includes playwriting, acting, and producing.
THE BENCH CONTACT INFORMATION Paula Fell (310) 497-6684 paulafell@cox.net 3520 Fifth Avenue Corona del Mar, CA 92625 BIOGRAPHY My experience in the theatre includes playwriting, acting, and producing.
STUCK. written by. Steve Meredith
 STUCK written by Steve Meredith StevenEMeredith@gmail.com Scripped scripped.com January 22, 2011 Copyright (c) 2011 Steve Meredith All Rights Reserved INT-OFFICE BUILDING-DAY A man and a woman wait for
STUCK written by Steve Meredith StevenEMeredith@gmail.com Scripped scripped.com January 22, 2011 Copyright (c) 2011 Steve Meredith All Rights Reserved INT-OFFICE BUILDING-DAY A man and a woman wait for
************************ CAT S IN THE CRADLE. him"
 CAT S IN THE CRADLE My child arrived just the other day He came to the world in the usual way But there were planes to catch and bills to pay He learned to walk while I was away And he was talkin' 'fore
CAT S IN THE CRADLE My child arrived just the other day He came to the world in the usual way But there were planes to catch and bills to pay He learned to walk while I was away And he was talkin' 'fore
Bereavement. Heaven Collins. 5/2/16 Bellows Free Academy Saint Albans 380 Lake Rd, Saint Albans, VT (802)
 Bereavement by Heaven Collins 5/2/16 Bellows Free Academy Saint Albans 380 Lake Rd, Saint Albans, VT 05478 (802) 370 5776 hlcollins@fcsuvt.org CHARACTERS:, Husband, 37, Wife, 36, always working, 78 SETTING:
Bereavement by Heaven Collins 5/2/16 Bellows Free Academy Saint Albans 380 Lake Rd, Saint Albans, VT 05478 (802) 370 5776 hlcollins@fcsuvt.org CHARACTERS:, Husband, 37, Wife, 36, always working, 78 SETTING:
Conversations with Logo (as overheard by Michael Tempel)
 www.logofoundation.org Conversations with Logo (as overheard by Michael Tempel) 1989 LCSI 1991 Logo Foundation You may copy and distribute this document for educational purposes provided that you do not
www.logofoundation.org Conversations with Logo (as overheard by Michael Tempel) 1989 LCSI 1991 Logo Foundation You may copy and distribute this document for educational purposes provided that you do not
Candice Bergen Transcript 7/18/06
 Candice Bergen Transcript 7/18/06 Candice, thank you for coming here. A pleasure. And I'm gonna start at the end, 'cause I'm gonna tell you I'm gonna start at the end. And I may even look tired. And the
Candice Bergen Transcript 7/18/06 Candice, thank you for coming here. A pleasure. And I'm gonna start at the end, 'cause I'm gonna tell you I'm gonna start at the end. And I may even look tired. And the
Victorian inventions - The telephone
 The Victorians Victorian inventions - The telephone Written by John Tuckey It s hard to believe that I helped to make the first ever version of a device which is so much part of our lives that why - it's
The Victorians Victorian inventions - The telephone Written by John Tuckey It s hard to believe that I helped to make the first ever version of a device which is so much part of our lives that why - it's
Mary Murphy: I want you to take out your diagrams that you drew yesterday.
 Learning Vocabulary in Biology Video Transcript Mary I want you to take out your diagrams that you drew yesterday. We are in the middle of a unit talking about protein synthesis, so today's class focused
Learning Vocabulary in Biology Video Transcript Mary I want you to take out your diagrams that you drew yesterday. We are in the middle of a unit talking about protein synthesis, so today's class focused
EXCERPT FROM WILLING OBJECTS BY SERAFINA DONAHUE
 EXCERPT FROM WILLING OBJECTS BY JAMIE: Is it raining out? KATELYN: (KATELYN nodding, stripping off her wet jacket) It just started when I got on the bus. JAMIE: Where's your umbrella? KATELYN: I left it
EXCERPT FROM WILLING OBJECTS BY JAMIE: Is it raining out? KATELYN: (KATELYN nodding, stripping off her wet jacket) It just started when I got on the bus. JAMIE: Where's your umbrella? KATELYN: I left it
2003 ENG Edited by
 2003 (This is NOT the actual test.) No.000001 0. ICU 1. PART,,, 4 2. PART 13 3. PART 12 4. PART 10 5. PART 2 6. PART 7. PART 8. 4 2003 Edited by www.bucho-net.com Edited by www.bucho-net.com Chose the
2003 (This is NOT the actual test.) No.000001 0. ICU 1. PART,,, 4 2. PART 13 3. PART 12 4. PART 10 5. PART 2 6. PART 7. PART 8. 4 2003 Edited by www.bucho-net.com Edited by www.bucho-net.com Chose the
And all that glitters is gold Only shooting stars break the mold. Gonna Be
 Allstar Somebody once told me the world is gonna roll me I ain't the sharpest tool in the shed She was looking kind of dumb with her finger and her thumb In the shape of an "L" on her forehead Well the
Allstar Somebody once told me the world is gonna roll me I ain't the sharpest tool in the shed She was looking kind of dumb with her finger and her thumb In the shape of an "L" on her forehead Well the
Lesson 25: Solving Problems in Two Ways Rates and Algebra
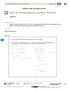 : Solving Problems in Two Ways Rates and Algebra Student Outcomes Students investigate a problem that can be solved by reasoning quantitatively and by creating equations in one variable. They compare the
: Solving Problems in Two Ways Rates and Algebra Student Outcomes Students investigate a problem that can be solved by reasoning quantitatively and by creating equations in one variable. They compare the
The Basics of Reading Music by Kevin Meixner
 The Basics of Reading Music by Kevin Meixner Introduction To better understand how to read music, maybe it is best to first ask ourselves: What is music exactly? Well, according to the 1976 edition (okay
The Basics of Reading Music by Kevin Meixner Introduction To better understand how to read music, maybe it is best to first ask ourselves: What is music exactly? Well, according to the 1976 edition (okay
NUMB3RS Activity: Coded Messages. Episode: The Mole
 Teacher Page 1 : Coded Messages Topic: Inverse Matrices Grade Level: 10-11 Objective: Students will learn how to apply inverse matrix multiplication to the coding of values. Time: 15 minutes Materials:
Teacher Page 1 : Coded Messages Topic: Inverse Matrices Grade Level: 10-11 Objective: Students will learn how to apply inverse matrix multiplication to the coding of values. Time: 15 minutes Materials:
Elementary Podcast 2-5 Transcript
 Transcript Download the LearnEnglish Elementary podcast. You ll find all the details on this page: http://learnenglish.britishcouncil.org/elementarypodcasts/series-02-episode-05 Section 1: "Well, that's
Transcript Download the LearnEnglish Elementary podcast. You ll find all the details on this page: http://learnenglish.britishcouncil.org/elementarypodcasts/series-02-episode-05 Section 1: "Well, that's
TAINTED LOVE. by WALTER WYKES CHARACTERS MAN BOY GIRL. SETTING A bare stage
 by WALTER WYKES CHARACTERS SETTING A bare stage CAUTION: Professionals and amateurs are hereby warned that Tainted Love is subject to a royalty. It is fully protected under the copyright laws of the United
by WALTER WYKES CHARACTERS SETTING A bare stage CAUTION: Professionals and amateurs are hereby warned that Tainted Love is subject to a royalty. It is fully protected under the copyright laws of the United
MITOCW watch?v=6wud_gp5wee
 MITOCW watch?v=6wud_gp5wee The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
MITOCW watch?v=6wud_gp5wee The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To
Sleeping Beauty By Camille Atebe
 Sleeping Beauty By Camille Atebe Characters Page Queen Constance Princess Aurora Good Fairies Bad Fairy Marlene Beatrice Prince Valiant Regina 2008 Camille Atebe Scene 1 Page Hear ye, hear ye, now enters
Sleeping Beauty By Camille Atebe Characters Page Queen Constance Princess Aurora Good Fairies Bad Fairy Marlene Beatrice Prince Valiant Regina 2008 Camille Atebe Scene 1 Page Hear ye, hear ye, now enters
1 MR. ROBERT LOPER: I have nothing. 3 THE COURT: Thank you. You're. 5 MS. BARNETT: May we approach? 7 (At the bench, off the record.
 167 April Palatino - March 7, 2010 Redirect Examination by Ms. Barnett 1 MR. ROBERT LOPER: I have nothing 2 further, Judge. 3 THE COURT: Thank you. You're 4 excused. 5 MS. BARNETT: May we approach? 6 THE
167 April Palatino - March 7, 2010 Redirect Examination by Ms. Barnett 1 MR. ROBERT LOPER: I have nothing 2 further, Judge. 3 THE COURT: Thank you. You're 4 excused. 5 MS. BARNETT: May we approach? 6 THE
Kaytee s Contest Problem https://www.nctm.org/pows/
 Pre-Algebra PoW Packet Kaytee s Contest Problem 16004 https://www.nctm.org/pows/ Welcome! This packet contains a copy of the problem, the answer check, our solutions, some teaching suggestions, and samples
Pre-Algebra PoW Packet Kaytee s Contest Problem 16004 https://www.nctm.org/pows/ Welcome! This packet contains a copy of the problem, the answer check, our solutions, some teaching suggestions, and samples
#029: UNDERSTAND PEOPLE WHO SPEAK ENGLISH WITH A STRONG ACCENT
 #029: UNDERSTAND PEOPLE WHO SPEAK ENGLISH WITH A STRONG ACCENT "Excuse me; I don't quite understand." "Could you please say that again?" Hi, everyone! I'm Georgiana, founder of SpeakEnglishPodcast.com.
#029: UNDERSTAND PEOPLE WHO SPEAK ENGLISH WITH A STRONG ACCENT "Excuse me; I don't quite understand." "Could you please say that again?" Hi, everyone! I'm Georgiana, founder of SpeakEnglishPodcast.com.
MORNING STORIES TRANSCRIPT
 MORNING STORIES TRANSCRIPT Behind the Blue Ribbon: Erica Ferencik couldn't find anything nice to say to eulogize her mother. Thanks to her mother's friends, she didn't have to. Hi everybody! This is Tony
MORNING STORIES TRANSCRIPT Behind the Blue Ribbon: Erica Ferencik couldn't find anything nice to say to eulogize her mother. Thanks to her mother's friends, she didn't have to. Hi everybody! This is Tony
MITOCW mit-5_95j-s09-lec07_300k_pano
 MITOCW mit-5_95j-s09-lec07_300k_pano The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for
MITOCW mit-5_95j-s09-lec07_300k_pano The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for
The Product of Two Negative Numbers 1
 1. The Story 1.1 Plus and minus as locations The Product of Two Negative Numbers 1 K. P. Mohanan 2 nd March 2009 When my daughter Ammu was seven years old, I introduced her to the concept of negative numbers
1. The Story 1.1 Plus and minus as locations The Product of Two Negative Numbers 1 K. P. Mohanan 2 nd March 2009 When my daughter Ammu was seven years old, I introduced her to the concept of negative numbers
A STUDY OF THE FUNCTION OF RHETORICAL QUESTIONS IN THE NOVEL FIVE ON A TREASURE ISLAND (A PRAGMATIC APPROACH)
 A STUDY OF THE FUNCTION OF RHETORICAL QUESTIONS IN THE NOVEL FIVE ON A TREASURE ISLAND (A PRAGMATIC APPROACH) Pathy Yulinda, M.R. Nababan, and Djatmika Postgraduate Program of Sebelas Maret University,
A STUDY OF THE FUNCTION OF RHETORICAL QUESTIONS IN THE NOVEL FIVE ON A TREASURE ISLAND (A PRAGMATIC APPROACH) Pathy Yulinda, M.R. Nababan, and Djatmika Postgraduate Program of Sebelas Maret University,
10:00:32 Ia is stubborn. We fight about TV and cleaning up. 10:00:39 What annoys me most is that she's so stubborn.
 Script in English YLE 2004 EBU Children s Documentary 10:00:10 Stop - No! Yes. - No! BETWEEN ME AND MY SISTER 10:00:19 My name is Ella. I'm eleven years old. 10:00:32 Ia is stubborn. We fight about TV
Script in English YLE 2004 EBU Children s Documentary 10:00:10 Stop - No! Yes. - No! BETWEEN ME AND MY SISTER 10:00:19 My name is Ella. I'm eleven years old. 10:00:32 Ia is stubborn. We fight about TV
BBC LEARNING ENGLISH 6 Minute English Lifts
 BBC LEARNING ENGLISH 6 Minute English Lifts NB: This is not a word-for-word transcript Hello and welcome to 6 Minute English. I'm and I'm. Hello. I'd like to start by asking how did you get up here to
BBC LEARNING ENGLISH 6 Minute English Lifts NB: This is not a word-for-word transcript Hello and welcome to 6 Minute English. I'm and I'm. Hello. I'd like to start by asking how did you get up here to
Math: Fractions and Decimals 105
 Math: Fractions and Decimals 105 Many students face fractions with trepidation; they re too hard, I don t understand. If this is you, there is no better tool to bring yourself back up to speed than a tape
Math: Fractions and Decimals 105 Many students face fractions with trepidation; they re too hard, I don t understand. If this is you, there is no better tool to bring yourself back up to speed than a tape
2 THE COURT: All right. You may. 4 MS. BARNETT: Thank you, Your Honor. 6 having been first duly sworn, testified as follows:
 138 Jonathan French- March 7, 2010 Recross-Examination by Mr. Robert Loper 1 (Witness sworn.) 2 THE COURT: All right. You may 3 proceed. 4 MS. BARNETT: Thank you, Your Honor. 5 APRIL PALATINO, 6 having
138 Jonathan French- March 7, 2010 Recross-Examination by Mr. Robert Loper 1 (Witness sworn.) 2 THE COURT: All right. You may 3 proceed. 4 MS. BARNETT: Thank you, Your Honor. 5 APRIL PALATINO, 6 having
Lexie World (The Three Lost Kids, #1) Chapter 1- Where My Socks Disappear
 Lexie World (The Three Lost Kids, #1) by Kimberly Kinrade Illustrated by Josh Evans Chapter 1- Where My Socks Disappear I slammed open the glass door and raced into my kitchen. The smells of dinner cooking
Lexie World (The Three Lost Kids, #1) by Kimberly Kinrade Illustrated by Josh Evans Chapter 1- Where My Socks Disappear I slammed open the glass door and raced into my kitchen. The smells of dinner cooking
WEB FORM F USING THE HELPING SKILLS SYSTEM FOR RESEARCH
 WEB FORM F USING THE HELPING SKILLS SYSTEM FOR RESEARCH This section presents materials that can be helpful to researchers who would like to use the helping skills system in research. This material is
WEB FORM F USING THE HELPING SKILLS SYSTEM FOR RESEARCH This section presents materials that can be helpful to researchers who would like to use the helping skills system in research. This material is
NATIONAL TRANSPORTATION SAFETY BOARD WASHINGTON, DC INTERVIEW TRANSCRIPT CLYDE ANTROBUS NOVEMBER 18, 1996
 DOCKET NO. SA- APPENDIX NATIONAL TRANSPORTATION SAFETY BOARD WASHINGTON, DC INTERVIEW TRANSCRIPT CLYDE ANTROBUS NOVEMBER, ( pages) -----------------x BEFORE THE UNITED STATES OF AMERICA NATIONAL TRANSPORTATION
DOCKET NO. SA- APPENDIX NATIONAL TRANSPORTATION SAFETY BOARD WASHINGTON, DC INTERVIEW TRANSCRIPT CLYDE ANTROBUS NOVEMBER, ( pages) -----------------x BEFORE THE UNITED STATES OF AMERICA NATIONAL TRANSPORTATION
JENS LYBERTH & MAX IRELAND INFORMANT'S ADDRESS: SPADINA ROAD LIBRARY
 DOCUMENT NAME/INFORMANT: STORYTELLING #2 WITH JENS LYBERTH & MAX IRELAND INFORMANT'S ADDRESS: INTERVIEW LOCATION: SOCIAL GATHERING TRIBE/NATION: INUIT/ONEIDA LANGUAGE: INUIT/ONEIDA/ENGLISH DATE OF INTERVIEW:
DOCUMENT NAME/INFORMANT: STORYTELLING #2 WITH JENS LYBERTH & MAX IRELAND INFORMANT'S ADDRESS: INTERVIEW LOCATION: SOCIAL GATHERING TRIBE/NATION: INUIT/ONEIDA LANGUAGE: INUIT/ONEIDA/ENGLISH DATE OF INTERVIEW:
Kaytee s Contest. Problem of the Week Teacher Packet. Answer Check
 Problem of the Week Teacher Packet Kaytee s Contest Farmer Kaytee brought one of her prize-winning cows to the state fair, along with its calf. In order to get people to stop and admire her cow, she thought
Problem of the Week Teacher Packet Kaytee s Contest Farmer Kaytee brought one of her prize-winning cows to the state fair, along with its calf. In order to get people to stop and admire her cow, she thought
ABBOTT AND COSTELLO By Jonathan Mayer
 ABBOTT AND COSTELLO By Jonathan Mayer Copyright 2009 by Jonathan Mayer, All rights reserved. ISBN: 1-60003-469-1 CAUTION: Professionals and amateurs are hereby warned that this Work is subject to a royalty.
ABBOTT AND COSTELLO By Jonathan Mayer Copyright 2009 by Jonathan Mayer, All rights reserved. ISBN: 1-60003-469-1 CAUTION: Professionals and amateurs are hereby warned that this Work is subject to a royalty.
Elementary Podcast 2-7 Transcript
 Transcript Download the LearnEnglish Elementary podcast. You'll find all the details on this page: http://learnenglish.britishcouncil.org/en/element ary-podcasts/series-02-episode-07 Section 1: "I've had
Transcript Download the LearnEnglish Elementary podcast. You'll find all the details on this page: http://learnenglish.britishcouncil.org/en/element ary-podcasts/series-02-episode-07 Section 1: "I've had
2 nd Int. Conf. CiiT, Molika, Dec CHAITIN ARTICLES
 2 nd Int. Conf. CiiT, Molika, 20-23.Dec.2001 93 CHAITIN ARTICLES D. Gligoroski, A. Dimovski Institute of Informatics, Faculty of Natural Sciences and Mathematics, Sts. Cyril and Methodius University, Arhimedova
2 nd Int. Conf. CiiT, Molika, 20-23.Dec.2001 93 CHAITIN ARTICLES D. Gligoroski, A. Dimovski Institute of Informatics, Faculty of Natural Sciences and Mathematics, Sts. Cyril and Methodius University, Arhimedova
FILED: NEW YORK COUNTY CLERK 09/15/ :53 PM INDEX NO /2017 NYSCEF DOC. NO. 71 RECEIVED NYSCEF: 09/15/2017 EXHIBIT I
 EXHIBIT I Page 9 2 Q. So I'll try to help you with that. 3 A. Okay. 4 Q. Okay. And do you recall when you 5 looked at the attachment to the consignment 6 agreement between your company and Ms. Lutz 7 that
EXHIBIT I Page 9 2 Q. So I'll try to help you with that. 3 A. Okay. 4 Q. Okay. And do you recall when you 5 looked at the attachment to the consignment 6 agreement between your company and Ms. Lutz 7 that
LUYỆN TẬP CHỨC NĂNG GIAO TIẾP 1 ID: LINK XEM LỜI GIẢI
 LUYỆN TẬP CHỨC NĂNG GIAO TIẾP 1 ID: 46147 LINK XEM LỜI GIẢI http://moon.vn/fileid/46147 Câu 1 [318207]: A: Would you like a coke? A. I like coke. Thanks B. It's ok. I'm proud of you. C. Yes, please. But
LUYỆN TẬP CHỨC NĂNG GIAO TIẾP 1 ID: 46147 LINK XEM LỜI GIẢI http://moon.vn/fileid/46147 Câu 1 [318207]: A: Would you like a coke? A. I like coke. Thanks B. It's ok. I'm proud of you. C. Yes, please. But
Sketch. How Shall We Say Good-Bye? Richard Trump. Volume 2, Number Article 16. Iowa State College
 Sketch Volume 2, Number 3 1936 Article 16 How Shall We Say Good-Bye? Richard Trump Iowa State College Copyright c 1936 by the authors. Sketch is produced by The Berkeley Electronic Press (bepress). http://lib.dr.iastate.edu/sketch
Sketch Volume 2, Number 3 1936 Article 16 How Shall We Say Good-Bye? Richard Trump Iowa State College Copyright c 1936 by the authors. Sketch is produced by The Berkeley Electronic Press (bepress). http://lib.dr.iastate.edu/sketch
A Charlie Brown Thanksgiving
 Scripts.com A Charlie Brown Thanksgiving By Charles M. Schulz Page 1/10 Charlie Brown. Oh, Charlie Brown. I can't believe it. She must think I'm the most stupid person alive. Come on, Charlie Brown. I'll
Scripts.com A Charlie Brown Thanksgiving By Charles M. Schulz Page 1/10 Charlie Brown. Oh, Charlie Brown. I can't believe it. She must think I'm the most stupid person alive. Come on, Charlie Brown. I'll
Proceedings of the Third International DERIVE/TI-92 Conference
 Description of the TI-92 Plus Module Doing Advanced Mathematics with the TI-92 Plus Module Carl Leinbach Gettysburg College Bert Waits Ohio State University leinbach@cs.gettysburg.edu waitsb@math.ohio-state.edu
Description of the TI-92 Plus Module Doing Advanced Mathematics with the TI-92 Plus Module Carl Leinbach Gettysburg College Bert Waits Ohio State University leinbach@cs.gettysburg.edu waitsb@math.ohio-state.edu
+ b ] and um we kept going like I think I got
![+ b ] and um we kept going like I think I got + b ] and um we kept going like I think I got](/thumbs/86/93211613.jpg) Page: 1 of 7 1 Stephanie And that s how you can get (inaudible) Should I keep going with that? 2 R2 Did you do that last night? 3 Stephanie Last 4 R2 Last time 5 Stephanie Um 6 R2 Did you carry it further?
Page: 1 of 7 1 Stephanie And that s how you can get (inaudible) Should I keep going with that? 2 R2 Did you do that last night? 3 Stephanie Last 4 R2 Last time 5 Stephanie Um 6 R2 Did you carry it further?
Episode 45: Making the Customer Journey Understandable and Efficient
 Experience This! Show Podcast Hosts: Joey Coleman & Dan Gingiss ExperienceThisShow.com [SHOW INTRO] Official Show Transcript Originally Aired: October 23, 2018 Episode 45: Making the Customer Journey Understandable
Experience This! Show Podcast Hosts: Joey Coleman & Dan Gingiss ExperienceThisShow.com [SHOW INTRO] Official Show Transcript Originally Aired: October 23, 2018 Episode 45: Making the Customer Journey Understandable
WJEC MATHEMATICS INTERMEDIATE ALGEBRA. SEQUENCES & Nth TERM
 WJEC MATHEMATICS INTERMEDIATE ALGEBRA SEQUENCES & Nth TERM 1 Contents Number Machines Continuing a sequence Finding the nth term Writing terms using the nth term Picture Sequences Credits WJEC Question
WJEC MATHEMATICS INTERMEDIATE ALGEBRA SEQUENCES & Nth TERM 1 Contents Number Machines Continuing a sequence Finding the nth term Writing terms using the nth term Picture Sequences Credits WJEC Question
Testimony of Kay Norris
 Testimony of Kay Norris DIRECT EXAMINATION 2 3 BY MS. SHERRI WALLACE: 4 Q. Ms. Norris, are you sick? 5 A. I am very sick. I have got strep 6 throat. 7 Q. I'm sorry you have to be down here. I 8 will try
Testimony of Kay Norris DIRECT EXAMINATION 2 3 BY MS. SHERRI WALLACE: 4 Q. Ms. Norris, are you sick? 5 A. I am very sick. I have got strep 6 throat. 7 Q. I'm sorry you have to be down here. I 8 will try
Effective Practice Briefings: Robert Sylwester 02 Page 1 of 10
 Effective Practice Briefings: Robert Sylwester 02 Page 1 of 10 I d like to welcome our listeners back to the second portion of our talk with Dr. Robert Sylwester. As we ve been talking about movement as
Effective Practice Briefings: Robert Sylwester 02 Page 1 of 10 I d like to welcome our listeners back to the second portion of our talk with Dr. Robert Sylwester. As we ve been talking about movement as
Condcnsclt! 11. Page 123 Page A. Johnnycake Road. 2 Q. And how close to the -- where Rolling Road. 3 crosses Johnnycake is it?
 Condcnsclt! 11 Page 123 Page 125 1 MS. GUTIERREZ: See, I object - 1 A. Johnnycake Road. 2 THE COURT: Overruled. 2 Q. And how close to the -- where Rolling Road 3 MS. GUTIERREZ: (Inaudible) objection. 3
Condcnsclt! 11 Page 123 Page 125 1 MS. GUTIERREZ: See, I object - 1 A. Johnnycake Road. 2 THE COURT: Overruled. 2 Q. And how close to the -- where Rolling Road 3 MS. GUTIERREZ: (Inaudible) objection. 3
For more material and information, please visit Tai Lieu Du Hoc at American English Idioms.
 101 American English Idioms (flee in a hurry) Poor Rich has always had his problems with the police. When he found out that they were after him again, he had to take it on the lamb. In order to avoid being
101 American English Idioms (flee in a hurry) Poor Rich has always had his problems with the police. When he found out that they were after him again, he had to take it on the lamb. In order to avoid being
STORY BY JON SCIESZKA PAINTINGS BY STEVE JOHNSON
 STORY BY JON SCIESZKA PAINTINGS BY STEVE JOHNSON PUFFIN BOOK" To Mom and Dad JS To our Grandparents for cookies, tree climbing, dancing, and frog hunts. S} and LF The Princess kissed the frog. He turned
STORY BY JON SCIESZKA PAINTINGS BY STEVE JOHNSON PUFFIN BOOK" To Mom and Dad JS To our Grandparents for cookies, tree climbing, dancing, and frog hunts. S} and LF The Princess kissed the frog. He turned
BBC Learning English 6 Minute English Reading the classics
 BBC Learning English 6 Minute English Reading the classics NB: This is not a word for word transcript Hello this is 6 Minute English, I'm Alice and today, I'm joined by Yvonne. Hello, Yvonne! Hello Alice!
BBC Learning English 6 Minute English Reading the classics NB: This is not a word for word transcript Hello this is 6 Minute English, I'm Alice and today, I'm joined by Yvonne. Hello, Yvonne! Hello Alice!
Aaah just some additional questions that-that we had and we wanted to talk to you in person, okay?
 November 11, 2014 1:14 p.m. Special Agent () Federal Bureau of Investigation = AU = AU DOJ Trial Attorney = Unintelligible= Ul AU Today is Wednesday, November l2 1 h, 2014, 1:14 p.m. I am Special Agent,
November 11, 2014 1:14 p.m. Special Agent () Federal Bureau of Investigation = AU = AU DOJ Trial Attorney = Unintelligible= Ul AU Today is Wednesday, November l2 1 h, 2014, 1:14 p.m. I am Special Agent,
Chapter X. In which Christopher Robin and pooh come to an enchanted place, and we leave them there
 Chapter X. In which Christopher Robin and pooh come to an enchanted place, and we leave them there CHRISTOPHER ROBIN was going away. Nobody knew why he was going; nobody knew where he was going; indeed,
Chapter X. In which Christopher Robin and pooh come to an enchanted place, and we leave them there CHRISTOPHER ROBIN was going away. Nobody knew why he was going; nobody knew where he was going; indeed,
WAITING. a short one act comedy for two actors. by claire demmer.
 WAITING a short one act comedy for two actors by claire demmer http://offthewallplays.com Waiting a one act comedy CHARACTERS: A very ordinary looking, slightly nerdy guy of any age A typical middle class
WAITING a short one act comedy for two actors by claire demmer http://offthewallplays.com Waiting a one act comedy CHARACTERS: A very ordinary looking, slightly nerdy guy of any age A typical middle class
Laplace Transform: basic properties; functions of a complex variable; poles diagrams; s-shift law.
 18.03 Lecture 26, April 14 Laplace Transform: basic properties; functions of a complex variable; poles diagrams; s-shift law. [1] The Laplace transform connects two worlds: The t domain t is real and positive
18.03 Lecture 26, April 14 Laplace Transform: basic properties; functions of a complex variable; poles diagrams; s-shift law. [1] The Laplace transform connects two worlds: The t domain t is real and positive
EXTRA in English Episode 12: Football Crazy Script
 EXTRA in English Episode 12: Football Crazy Script COMMENTARY [v.o.] This is the story of Bridget and Annie who share a flat in London and the boys next door, Nick and his friend Hector from Argentina.
EXTRA in English Episode 12: Football Crazy Script COMMENTARY [v.o.] This is the story of Bridget and Annie who share a flat in London and the boys next door, Nick and his friend Hector from Argentina.
ART IMITATES LIFE. By Mike McCafferty. Copyright MMIX by Mike McCafferty All Rights Reserved Heuer Publishing LLC, Cedar Rapids, Iowa
 ART IMITATES LIFE TEN-MINUTE PLAY By Mike McCafferty All Rights Reserved Heuer Publishing LLC, Cedar Rapids, Iowa The writing of plays is a means of livelihood. Unlawful use of a playwright s work deprives
ART IMITATES LIFE TEN-MINUTE PLAY By Mike McCafferty All Rights Reserved Heuer Publishing LLC, Cedar Rapids, Iowa The writing of plays is a means of livelihood. Unlawful use of a playwright s work deprives
Date: Thursday, 18 November :00AM
 The Composer Virtuoso - Liszt s Transcendental Studies Transcript Date: Thursday, 18 November 2004-12:00AM THE COMPOSER VIRTUOSO: LISZT'S TRANSCENDENTAL STUDIES Professor Adrian Thomas I'm joined today
The Composer Virtuoso - Liszt s Transcendental Studies Transcript Date: Thursday, 18 November 2004-12:00AM THE COMPOSER VIRTUOSO: LISZT'S TRANSCENDENTAL STUDIES Professor Adrian Thomas I'm joined today
Barbara Gillman: Gallery Owner, Lincoln Road, brought Andy Warhol to Miami Beach
 Interviewee: Interviewer: Location: Barbara Gillman: Gallery Owner, Lincoln Road, brought Andy Warhol to Miami Beach Kathy Hersh 1001 Ocean Drive, Miami Beach, FL Date Recorded: 2/18/12 Q: Barbara, you
Interviewee: Interviewer: Location: Barbara Gillman: Gallery Owner, Lincoln Road, brought Andy Warhol to Miami Beach Kathy Hersh 1001 Ocean Drive, Miami Beach, FL Date Recorded: 2/18/12 Q: Barbara, you
6.034 Notes: Section 4.1
 6.034 Notes: Section 4.1 Slide 4.1.1 What is a logic? A logic is a formal language. And what does that mean? It has a syntax and a semantics, and a way of manipulating expressions in the language. We'll
6.034 Notes: Section 4.1 Slide 4.1.1 What is a logic? A logic is a formal language. And what does that mean? It has a syntax and a semantics, and a way of manipulating expressions in the language. We'll
